线性代数-相似矩阵和若尔当型-29

Linear Algebra-相似矩阵和若尔当型-29

一、知识概要

本节从回顾正定矩阵相关知识出发，介绍了相似矩阵和若尔当型的概念。内容侧重于让读者对这些矩阵变换方式有初步的认识，未进行深入探讨。

二、正定矩阵补充

基于上一节学习的正定矩阵知识，探讨以下几个问题：

(1) 正定矩阵的逆矩阵是否也是正定矩阵？

解：因为逆矩阵的特征值是原矩阵特征值的倒数，所以若$A$是正定矩阵，那么$A^{-1}$的特征值也都为正，故$A^{-1}$也是正定矩阵。

(2) 假定$A$和$B$是正定矩阵，那么$A + B$呢？

解：由于$A$、$B$正定，根据正定矩阵判据式可得$x^{T}Ax > 0$，$x^{T}Bx > 0$。

于是$x^{T}(A + B)x = x^{T}Ax + x^{T}Bx > 0$，所以，若$A$、$B$都是正定矩阵，则$A + B$也是正定矩阵。

(3) 假设$A$是$m×n$长方形矩阵，$A^{T}A$是否是一个正定矩阵？

解：使用正定矩阵判据式$x^{T}A^{T}A x$，可得$(Ax)^{T}Ax = |Ax|^{2}$ 。

当$A$的各列向量线性无关（零空间只有零向量），即仅当$x$为零向量时，$Ax = 0$，此时$|Ax|^{2}>0$ 。

也就是说，矩阵$A$各列线性无关，列满秩时，可以确保$A^{T}A$是正定矩阵。

对于正定矩阵，不需要进行“行交换”，也不必担心主元过小或者等于零，这能简化很多计算。

三、相似矩阵

对于两个$n$阶方阵$A$和$B$，若两者相似，则存在某个可逆矩阵$M$，使得等式$B = M^{-1}AM$成立。

【例】设$A$具有无关的特征向量，由前面知识可知$S^{-1}AS = \Lambda$ ，按照相似矩阵定义，$A$与$\Lambda$相似。但与$A$相似的不只是对角阵，任取一对矩阵与矩阵的逆，都可计算与$A$相似的矩阵。

例如：假设$A=\begin{bmatrix}2 & 1\\1 & 2\end{bmatrix}$ ，其特征值为 $1$、$3$。

任取一对矩阵与矩阵的逆计算与$A$相似的矩阵：

$$M^{-1}AM = \begin{bmatrix}1 & -4\\0 & 1\end{bmatrix} \begin{bmatrix}2 & 1\\1 & 2\end{bmatrix} \begin{bmatrix}1 & 4\\0 & 1\end{bmatrix} =\begin{bmatrix}-2 & -15\\1 & 6\end{bmatrix}$$

最终得到的矩阵$B$就与矩阵$A$相似。

那么矩阵$B$与$A$有什么共同性质呢？答案是：它们具有相同的特征值（计算$B$的特征值可以验证这一结论）。

结论：相似矩阵特征值相同（事实上，其线性无关的特征向量数目也一样）。

证明：

• 首先写出特征方程$Ax = \lambda x$ ，因为$A = A I = AMM^{-1}$，所以$AMM^{-1}x = \lambda x$ 。
• 同时左乘$M^{-1}$得到：$M^{-1}AMM^{-1}x = M^{-1}\lambda x$ 。
• 由$B = M^{-1}AM$可得：$BM^{-1}x = \lambda M^{-1}x$ 。

这就说明了$A$与$B$特征值相同，线性无关的特征向量数目也相同。但是特征向量不一定相同（$B$的特征向量对应为$M^{-1}x$ ）。

四、若尔当型

4.1 重特征值的相似情况

上面介绍相似矩阵时提到，相似矩阵的特征值相同。那么，特征值相同的矩阵是否都属于同一类呢？下面通过二阶矩阵进行讨论：

设$\lambda_{1}=\lambda_{2}=4$ ，具有此特征值的二阶矩阵可以被分为两类：

(1) $\begin{bmatrix}4 & 0\\0 & 4\end{bmatrix}$ 自己是一类，也就是说，这类只有一个矩阵。

$$M^{-1}\begin{bmatrix}4 & 0\\0 & 4\end{bmatrix}M = 4M^{-1}IM = \begin{bmatrix}4 & 0\\0 & 4\end{bmatrix}$$

由上述相似运算过程可知，与$\begin{bmatrix}4 & 0\\0 & 4\end{bmatrix}$相似的只有其自身。

(2)其他特征值为 $4$ 的矩阵是另一类，例如$\begin{bmatrix}4 & 1\\0 & 4\end{bmatrix}$ 、$\begin{bmatrix}5 & 1\\ -1 & 3\end{bmatrix}$ 、$\begin{bmatrix}a & *\\ * & 8 - a\end{bmatrix}$ ，其中最有代表性的是$\begin{bmatrix}4 & 1\\0 & 4\end{bmatrix}$ ，我们称之为若尔当标准型。而这一类矩阵不可以相似对角化（否则就与第一类相似了）。

结论：对于之前不能完成相似对角化的矩阵，都可以通过某种特殊方法，完成近似的“对角化”，比如若尔当标准型。

4.2 若尔当型

由 4.1 可知，若尔当型出现的背景是特征值相同，但矩阵不相似的情况。接下来举两个具有四重根的例子：

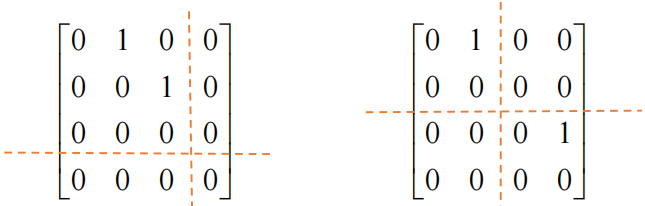
【例 1】给定矩阵：

$$\begin{bmatrix}0 & 1 & 0 & 0\\0 & 0 & 1 & 0\\0 & 0 & 0 & 0\\0 & 0 & 0 & 0\end{bmatrix}$$

分析：这个矩阵的四个特征值都是 $0$，对应的无关特征向量是两个，零空间的维数为$n - r = 4 - 2 = 2$ 。所以$Ax = 0$的解空间是二维的，$A$有两个特征向量。

【例 2】给定矩阵：

$$\begin{bmatrix}0 & 1 & 0 & 0\\0 & 0 & 0 & 0\\0 & 0 & 0 & 1\\0 & 0 & 0 & 0\end{bmatrix}$$

分析：这个矩阵的四个特征值同样都是 $0$，也有两个特征向量，但是，此时这个矩阵与【例 1】的矩阵并不相似。

接下来引入若尔当块的概念，通过若尔当块可以发现【例 1】和【例 2】的矩阵不相似，因为它们的若尔当块不一样。

若尔当块：$J_{i}$表示$i$阶的若尔当块，它只有一个重复的特征值，满足形式：

$$J_{i}=\begin{bmatrix}\lambda_{i} & 1 & 0 & 0\\0 & \lambda_{i} & \cdots & 0\\0 & \cdots & \cdots & 1\\0 & 0 & 0 & \lambda_{i}\end{bmatrix}$$

解释：若尔当块的对角线上都是同一个数，即重特征值$\lambda_{i}$ 。而对角线元素上方的第一个元素为 $1$，矩阵其余元素皆为 $0$。

另外注意，若尔当块的特征向量只有一个。若尔当块可以构成若尔当矩阵，形如：

$$J=\begin{bmatrix}[J_{1}] & & \\ & \cdots & \\ & & [J_{d}]\end{bmatrix}$$

其中：

(1)若尔当块的个数等于矩阵特征向量的个数，因为每一块对应于一个特征向量。

(2)如果矩阵的特征值不相同，那么它就是一个可对角化的矩阵（对应的图中的$d$就是$n$），所对应的若尔当阵就是对角阵$\Lambda$ 。

(3)每个方阵都相似于一个若尔当阵$J$ 。

从之前的例子中的两个矩阵可以找到若尔当块，由于这两个矩阵的若尔当块的分块不一样，所以【例 1】与【例 2】的矩阵是不相似的。

本节课未对如何求得若尔当矩阵展开详细讨论。

4.3 应用场景

其实也谈不上什么应用，只是说在面对一些性质不太好的方阵的时候，只能采用近似对角化的形式$A=MJM^{-1}$($J$是 Jordan Matrix,不是对角阵; $M$是可逆矩阵)。

所以，对于任意方阵$A$，如果我们要计算$A^k$又正好碰上不能对角化的情况，我们就可以使用其近似对角化形式$\bf A^k=MJ^kM^{-1}$ 计算。

但是，Jordan 标准型实际应用的场景不如前文介绍的对角化或者正交对角化广泛，因为用他的计算不稳定。

五、学习感悟

本节介绍了相似矩阵和若尔当块的相关知识，从正反两方面探讨了矩阵相似时对应的特征值情况，进而引出了若尔当阵的判断方法。不过，对于若尔当矩阵的求解过程并未深入了解。

需要记住最重要的结论：相似矩阵的特征值相同。