线性代数-正定矩阵和最小值-28

Linear Algebra-正定矩阵和最小值-28

一、知识概要

本节围绕正定矩阵展开，将主元、行列式、特征值等之前所学知识联系起来。通过正定矩阵的判据式 $x^{T}Ax$ ，引出矩阵与函数之间的关系和对应特点，介绍如何利用正定矩阵找到函数最小值，并绘制对应函数图像，从几何角度进行解释。

二、正定矩阵

我们从研究 $2\times2$ 的对称矩阵开始：

设 $A=\begin{bmatrix}a & b\\b & c\end{bmatrix}$ ，判断其是否为正定矩阵有以下 4 种判定方法：

1. 特征值判定：$\lambda_{1}>0$ ，$\lambda_{2}>0$ ，即矩阵的所有特征值都为正数。
2. 行列式判定：$a >0$ ，$ac - b^{2}>0$ ，也就是顺序主子式均为正值。
3. 主元判定：$a >0$ ，$\frac{ac - b^{2}}{a}>0$ ，意味着主元都为正数。
4. 判据式：$x^{T}Ax>0$ 。

需要注意的是，在线性代数范围内，正定矩阵必须是对称阵。

例如矩阵 $A=\begin{bmatrix}2 & 6\\6 &?\end{bmatrix}$ ，当“?”处填入 18 以上的整数时，该矩阵为正定矩阵。若“?”处恰好填 18，此时矩阵行列式为 0，这样的$A$矩阵称为半正定矩阵。它只有一个主元 2，并且 $A$ 是奇异矩阵，特征值为 0 和 20，都大于等于 0 。

接下来围绕最重要的判据式 $x^{T}Ax>0$ 展开讨论。

先看 $A=\begin{bmatrix}2 & 6\\6 & 18\end{bmatrix}$ 这个半正定的情况，根据判据式可得：

$$\begin{array}{r} x^{T}Ax=\begin{bmatrix}x_{1} & x_{2}\end{bmatrix}\begin{bmatrix}2 & 6\\6 & 18\end{bmatrix}\begin{bmatrix}x_{1}\\x_{2}\end{bmatrix}=2x_{1}^{2}+12x_{1}x_{2}+18x_{2}^{2} \\ \end{array}$$

可以看到，$x_{1}^{2}$ ，$x_{1}x_{2}$ ，$x_{2}^{2}$ 前的系数分别为矩阵 $\begin{bmatrix}a & b\\b & c\end{bmatrix}$ 中的 $a$ 、 $2b$ 、 $c$ ，这就是二次型。判断 $A$ 是不是正定矩阵，就是判别由 $x^{T}Ax$ 构造出的类似 $2x_{1}^{2}+12x_{1}x_{2}+18x_{2}^{2}$ 的二次型是否恒大于 0 。对于 $2x_{1}^{2}+12x_{1}x_{2}+18x_{2}^{2}$ ，它显然不是恒正的，因为在某些取值情况下，其结果可以为 0 。

这表明，当 $A$ 为半正定时，其对应的二次型在某些情况下会得到 0 。那么当 $A$ 不是正定时，其对应的 $x^{T}Ax$ 会呈现出什么状态呢？

取 $A=\begin{bmatrix}2 & 6\\6 & 7\end{bmatrix}$ 观察，此时得到的二次型为：

$$x^{T}Ax=2x_{1}^{2}+12x_{1}x_{2}+7x_{2}^{2}$$

将其看作函数 $f(x, y)=2x^{2}+12xy + 7y^{2}$ ，绘制在坐标轴中得到一个马鞍面。其中有一个鞍点，从不同方向观察，它在某个方向上是极大值，在另一个方向上是极小值。最佳观测方向是沿特征向量的方向。显然此时的 $A$ 不是一个正定矩阵。

% 定义x和y的取值范围
x = -5:0.1:5;
y = -5:0.1:5;

% 生成网格数据
[X,Y] = meshgrid(x,y);

% 计算函数值
Z = 2*X.^2 + 12*X.*Y + 7*Y.^2;

% 绘制三维曲面
surf(X,Y,Z);
shading interp; % 使颜色过渡更平滑
title('f(x, y)=2x^{2}+12xy + 7y^{2}');
xlabel('x');
ylabel('y');
zlabel('f(x, y)');

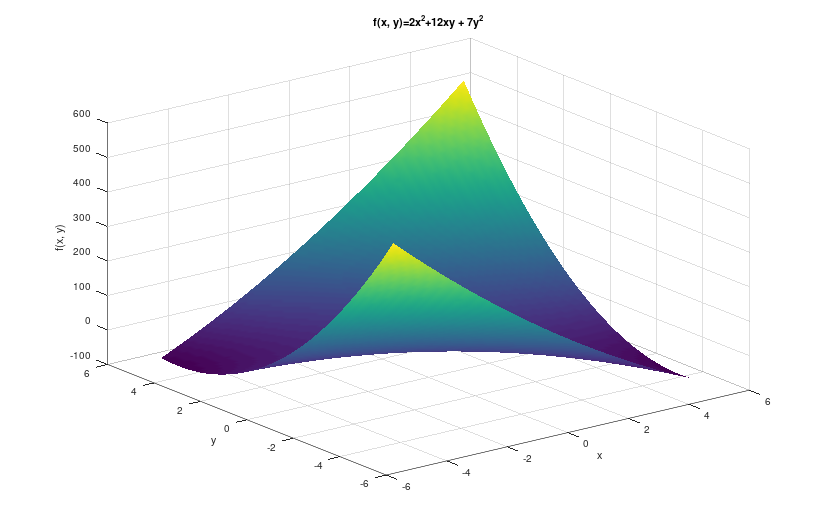
说完半正定与非正定矩阵，再举一个正定矩阵的例子，并探讨它的特点以及二次型与正定矩阵之间的联系。

取矩阵 $A=\begin{bmatrix}2 & 6\\6 & 20\end{bmatrix}$ ，根据上述判据，很容易判断这是一个正定矩阵。重点看判据式 $x^{T}Ax$ ，经计算，它的二次型为：

$$x^{T}Ax=2x_{1}^{2}+12x_{1}x_{2}+20x_{2}^{2}$$

写成函数形式就是：

$$f(x, y)=2x^{2}+12xy + 20y^{2}$$

其图像切面类似二次函数。

很明显，$f(x, y)=2x^{2}+12xy + 20y^{2}$ 的极小值点在原点位置。根据微积分知识，原点处一阶偏导数为 0，二阶偏导数大于 0，所以可判断其为最小值点。也就是说，在微积分中，通过求导判断是否大于 0 来判断是否有最小值；在线性代数中，则通过判断二阶导数矩阵是否为正定来判断是否有最小值，这是正定矩阵的用法之一，即将数字问题转化为矩阵问题。

另外，对 $f(x, y)$ 进行配方：

$$f(x, y)=2x^{2}+12xy + 20y^{2}=2(x + 3y)^{2}+2y^{2}$$

容易想到，如果 $A$ 不是正定的，那么 $y^{2}$ 前的系数可能为负数。用 $f = 1$ 这个平面去截这个曲线，$f(x, y)=2x^{2}+12xy + 20y^{2}$ 截得的图形就是椭圆。

这里还要介绍，配方法在线代中对应着消元。对于 $A=\begin{bmatrix}2 & 6\\6 & 20\end{bmatrix}$ ，矩阵中的每一个元素都表示着 $f(x, y)$ 中对应项前的系数，经过消元，得到消元后的矩阵为 $\begin{bmatrix}2 & 6\\0 & 2\end{bmatrix}$ ，它们之间的关系为：

$2(x + 3y)^{2}+2y^{2}$ 与 $\begin{bmatrix}2 & 6\\6 & 20\end{bmatrix}=\begin{bmatrix}1 & 0\\3 & 1\end{bmatrix} \times\begin{bmatrix}2 & 6\\0 & 2\end{bmatrix}$

可以看出，括号外的系数就是主元，这样就将各个知识点联系起来了：正定意味着主元为正，进而二次型平方项外系数为正，图像朝上，原点为最小值点。

此理论可推广到 $n$ 维。同样，在微积分中学习二阶偏导数极值时的 $f_{xx}$ ，$f_{yy}$ 与 $(f_{xy})^{2}$ 之间的关系也能反映到矩阵的正定判断上，即矩阵 $\begin{bmatrix}f_{xx} & f_{xy}\\f_{yx} & f_{yy}\end{bmatrix}$ ，这就是二阶导数矩阵，它是将原来的 $\begin{bmatrix}2x^{2} & 6xy\\6xy & 20y^{2}\end{bmatrix}$ 对应元素求导得到的。判定是否有极小值的条件就是判断它是否为正定矩阵，这个判断同样可以推广到 $n\times n$ 的矩阵中。

我们再举一个 3 维椭球体与矩阵联系得到的特殊性质的例子：对于矩阵 $A=\begin{bmatrix}2 & -1 & 0\\ -1 & 2 & -1\\0 & -1 & 2\end{bmatrix}$ ，判断这个矩阵反映的性质。

很容易判断这个矩阵是一个正定矩阵，写出其二次型：

$$x^{T}Ax=2x_{1}^{2}+2x_{2}^{2}+2x_{3}^{2}-2x_{1}x_{2}-2x_{2}x_{3}$$

沿用上述方法，截出一个椭球体 $2x_{1}^{2}+2x_{2}^{2}+2x_{3}^{2}-2x_{1}x_{2}-2x_{2}x_{3}=1$ ，这时此椭球体的三个轴的方向即为 $A$ 矩阵的特征向量方向，三个轴的长度即为特征值的大小。我们可以通过分解 $A$ 矩阵：$A = Q\Lambda Q^{T}$ 得到对应值，这个特殊的性质被称为主轴定理。

对于三条判据可以判定正定： $x^TAx>0$ （x=0 除外）。已经分析了主元要大于零的原因，因为它是配方后的参数，只有都大于零才能保证正定。以下对于判据 1 做简要说明。
对称矩阵 A，其正交的特征向量可以张成整个空间，因此任意向量 x 均可表示成特征向量的线性组合 $x=c_1x_1+c_2x_2+…c_nx_n$ ，代入得$x^TAx=c_1^2λ_1x_1^2+c_2^2λ_2x_2^2+…c_n^2λ_nx_n^2$ ，当特征值都大于零且 x≠0 时，才能保证$x^TAx>0$。因此条件 1 与正定性等价。

三、学习感悟

本节从学习正定矩阵的判定方法入手，主要研究了判定式 $x^{T}Ax$ 的二次型及其在具体函数上所表现出的性质。这一节将微积分中的二阶导判定方法以及几何角度的图像走势与正定矩阵联系起来，让我们学会运用正定矩阵解决更多实际问题。

四、学习总结

1. 正定矩阵所有的特征值和主元都是正数；
2. 如果$A$的列向量线性无关，则$S=A^TA$是正定矩阵；