线性代数-微分方程和矩阵指数-23

Linear Algebra-微分方程和矩阵指数-23

一、知识概要

本节介绍一阶线性常微分方程的矩阵解法，也就是将微分方程用矩阵抽象，通过“解耦”，计算出对应系数，最终得到解。这里会牵涉到 $e^{At}$ 计算问题（A 是矩阵），所以也会引出幂指数是矩阵时算式的计算问题。最后扩展介绍了高阶微分方程的降阶求解方法。

二、解微分方程

解决微分方程问题重点在于其流程，我们通过一道例题来介绍本部分内容。

【例 1】：

$$\frac{d u_{1}}{dt}=-u_{1}+2 u_{2};\frac{d u_{2}}{dt}=u_{1}-2 u_{2};u(0)=\begin{bmatrix}1 \\ 0\end{bmatrix}$$

求 u(t) 。

解题之前首先要搞清楚这个微分方程的意义，我们看到，$u(0)=\begin{bmatrix}1 \\ 0\end{bmatrix}$，就是说明在最初 0 时刻，$u_{1}=1$，所有的值都在$u_{1}$中；而此时$u_{2}=0$，但是随着时间流逝，t 增加时，我们可以看到$\frac{d u_{2}}{dt}>0$ 。说明$u_{2}$的导数大于 0，$u_{2}$会慢慢增加，$u_{1}$慢慢减少（或者理解为$u_{1}$中的值流向$u_{2}$）。最终达到某一状态，这需要我们计算来得到。

列出方程$\frac{d u}{d t}=A u$，其中系数矩阵 A 应综合$\frac{d u_{1}}{dt}$与$\frac{d u_{2}}{d t}$，写做$\begin{bmatrix}-1 & 2 \\ 1 & -2\end{bmatrix}$ 。我们先给出通解形式：

$$\sum_{i=1}^{n} C_{i} e^{\lambda_{i} t} x_{i}$$

通解形式是如何得到的我们不做研究。具体验证可以将通解看做几个纯指数解的组合，随便挑一个代入验证一下即可。

解 A 矩阵的特征值与特征向量。不难得到这个矩阵有两个特征值：$\lambda_{1}=0$，$\lambda_{2}=-3$ 。特征向量为：$x_{1}=\begin{bmatrix}2 \\ 1\end{bmatrix}$，$x_{2}=\begin{bmatrix}1 \\ -1\end{bmatrix}$，代入通解得到其形式如下：

$$u(t)=C_{1} e^{0 t}\begin{bmatrix} 2 \\ 1 \end{bmatrix}+C_{2} e^{-3 t}\begin{bmatrix} 1 \\ -1 \end{bmatrix}$$

再代入初值$u(0)=\begin{bmatrix}1 \\ 0\end{bmatrix}$，确定$C_{1}$与$C_{2}$，最终解为：

$$u(t)=\frac{1}{3}\begin{bmatrix} 2 \\ 1 \end{bmatrix}+\frac{1}{3} e^{-3 t}\begin{bmatrix} 1 \\ -1 \end{bmatrix}$$

分析这个通解，我们发现随着时间 t 的增加，后一项$\frac{1}{3} e^{-3 t}\begin{bmatrix}1 \\ -1\end{bmatrix}$逐渐衰减，最后趋于 0，而前一项$\frac{1}{3}\begin{bmatrix}2 \\ 1\end{bmatrix}$不随时间改变，这也符合我们一开始分析微分方程意义的时候 u 的走势。

通过这道题，我们可以得到解决微分方程过程中遇到的某些特点：

(1)特征值是负数时，$u(t)$趋于 0。这个特点很简单，但是要注意一种特殊情况，就是特征值为复数时，$a + bi$怎么去判断$u(t)$的趋势呢？答案是只有实数部分决定$u(t)$趋势。我们可以画一个复数坐标系：

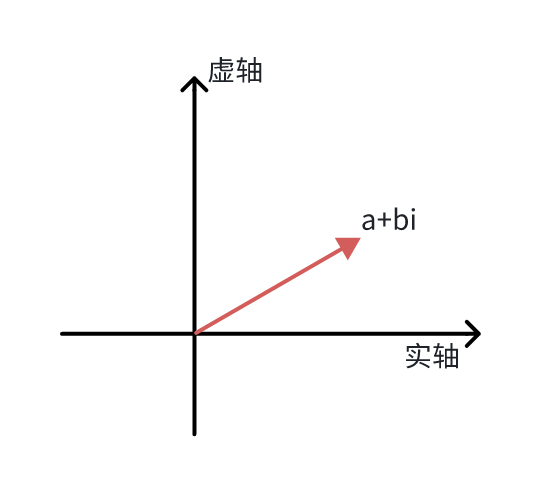
不难看出，投影到实数轴，只有实数部分$a$决定正负性，而虚部$b$的作用是在另一条轴上指明方向，所以不影响我们的判断。

(2)稳态存在时（如【例 1】中最后 t 趋于无穷时，u 趋于一个确数），一个特征向量$=0$，其余的特征向量全部$<0$。

(3)如果有任何特征值实数部分$>0$，则解无法收敛。

三、解耦与 $e^{A t}$

3.1 解耦

回到【例 1】，$\frac{d u}{d t}=A u$，矩阵 A 中，有$u_{1}$，$u_{2}$耦合，我们的处理，就是计算出特征值与特征向量将 A 解耦。我们设 S 是特征向量矩阵。

令$u = SV$，

$$\frac{d u}{d t}=S \frac{d v}{d t}=A u=A S V$$

提取出$S$得$\frac{d v}{d t}=A S V$ 。

两边同时左乘上$S^{-1}$，得到：$\frac{dv}{dt}=S^{-1} ASV=\Lambda V$，得到关于 V 的对角化方程组。新方程不耦合，$\frac{d v_{1}}{dt}=\lambda_{1} v_{1}$，$\frac{d v_{2}}{dt}=\lambda_{2} v_{2}$ 以此类推。最终可得到：

$$v(t)=e^{\Lambda t} v(0)$$

同类型地，也有：$u(t) = e^{At}u(0) = S e^{\Lambda t} S^{-1}u(0)$ 。这里就牵扯到了一个新问题，$e^{A_{t}}$和$e^{\Lambda t}$是什么？表面来看，$e^{At}$就是$u(t)$的解，那么$e^{At}$为什么与$S e^{\Lambda t} S^{-1}$相等呢？它们表示的是什么呢？我们接下来的重点就在介绍这些式子上。

3.2 $e^{At}$ 与 $S(e^{\Lambda t}) S^{-1}$

首先熟悉一下幂级数公式：

$$e^{x}=1+x+\frac{x^{2}}{2}+\frac{x^{3}}{6}+\cdots \cdots+\frac{x^{n}}{n!}+\cdots \cdots$$

（收敛域是全体实数，不用考虑特征值问题）

扩展到矩阵的计算中，同样，I 代替 1，矩阵代替 x，得到：

$$e^{A t}=I+A t+\frac{(A t)^{2}}{2}+\frac{(A t)^{3}}{6}+\cdots \cdots+\frac{(A t)^{n}}{n!}+\cdots \cdots$$

接下来我们对角化形式化简 A，得到

$$e^{A t}=S S^{-1}+S \Lambda t S^{-1}+\frac{S(\Lambda t)^{2} S^{-1}}{2}+\frac{S(\Lambda t)^{3} S^{-1}}{6}+\cdots \cdots$$

提出 S 和$S^{-1}$，得到：

$$e^{A t}=S\left(I+\Lambda t+\frac{(\Lambda t)^{2}}{2}+\frac{(\Lambda t)^{3}}{6}+\cdots \cdots\right) S^{-1}$$

综合幂级数公式，得到：$e^{A t}=S(e^{\Lambda t}) S^{-1}$。

注意：这步的化简是有条件的，即 A 必须可以对角化，即有 n 个独立的特征向量，$S^{-1}$存在。

3.3 矩阵指数

上面的等式将对角矩阵与一般矩阵联系了起来，那么其中的$e^{\Lambda t}$代表着什么呢？

我们知道$\Lambda=\begin{bmatrix}\lambda_{1} & 0 & \cdots & 0 \\ & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_{n}\end{bmatrix}$

那么$e^{\Lambda t}$就可以如下表示：

$$\begin{bmatrix} e^{\lambda_{1} t} & 0 & 0 & 0 \\ 0 & e^{\lambda_{2} t} & \cdots & 0 \\ \vdots & 0 & \ddots & \vdots \\ 0 & 0 & 0 & e^{\lambda_{n} t} \end{bmatrix}$$

其主对角线上皆为$e^{\lambda_{i} t}$，其余位置为 0。同样，这里的判断是否收敛与微分方程中的判别差不多，即比较$\lambda$的实部的绝对值与 1 的大小关系。

四、二阶微分方程的解

解二阶微分方程时，我们可以将它降阶处理，步骤如下：

二阶微分方程$y^{\prime \prime}+b y'+k y=0$

设$u=\begin{bmatrix}y' \\ y\end{bmatrix}$，可利用 u 将上面的方程化简为：

$$u'=\begin{bmatrix} y'' \\ y' \end{bmatrix}=\begin{bmatrix} -b & -k \\ 1 & 0 \end{bmatrix}\begin{bmatrix} y' \\ y \end{bmatrix}$$

这样我们就将二阶微分方程化简为了一阶微分方程乘上一个矩阵。同样，如果是求解一个五阶微分方程的话，我们只需要像上面那样化简，只不过其中$\begin{bmatrix}-b & -k \\ 1 & 0\end{bmatrix}$会变成一个 5×5 的矩阵，类似于$\begin{bmatrix}a & b & c & d & e \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0\end{bmatrix}$的矩阵，其中 a、b、c、d、e 都是方程中的系数，而且主对角线上的元素下的元素都是 0。这样的矩阵将五阶微分方程转化为一阶向量方程。接下来只要使用一阶微分方程正常求解就可以了。

五、学习感悟

本节内容较多，主要目的是在实际情况下使用矩阵对角化、特征值等方法求解微分方程，给出了一种使用矩阵求解微分方程的通用规律，即高阶降阶，一阶用特征值和特征向量将原系数矩阵 A 解耦，最后得到结果。并介绍了在我们解耦 A 时使用矩阵对角化将其与特征向量联系起来运算的方法。另外介绍了判断收敛性的方法，即看特征值实部绝对值与 1 的大小关系。这些内容都是特征值与特征向量的实际应用，较为重要。