线性代数-特征值和特征向量-21

Linear Algebra-特征值和特征向量-21

一、知识概要

本节课讨论了特征值与特征向量。主要目的是掌握求特征值的技巧并对一些特别的情况进行说明。本节内容比较基础。

二、特征值与特征向量

2.1 释义

首先给出特征值与特征向量的定义：对矩阵 A，若有

$$Ax=\lambda x$$

则 x 为矩阵 A 的特征向量，λ 为矩阵的特征值。那么如何理解特征值与特征向量所代表的意义呢？

我们来看$Ax$这个式子，对于不同的向量 x，$Ax$这个式子像是一个函数，输入一个向量 x，则输出一个向量$Ax$ 。而在我们输入的众多向量 x 生成的$Ax$中，会有这样的向量$Ax$，它们平行于 x，我们即用上面这个式子：$Ax=\lambda x$来表示这个关系。

特别注意下特征值为 0 的情况。此时会有：$AX = 0$。我们可以发现 A 如果是不可逆矩阵，则正好满足此性质。

我们再研究一下之前提到过的投影矩阵，如果投影矩阵是 A 的话，那么它的特征值是多少呢？

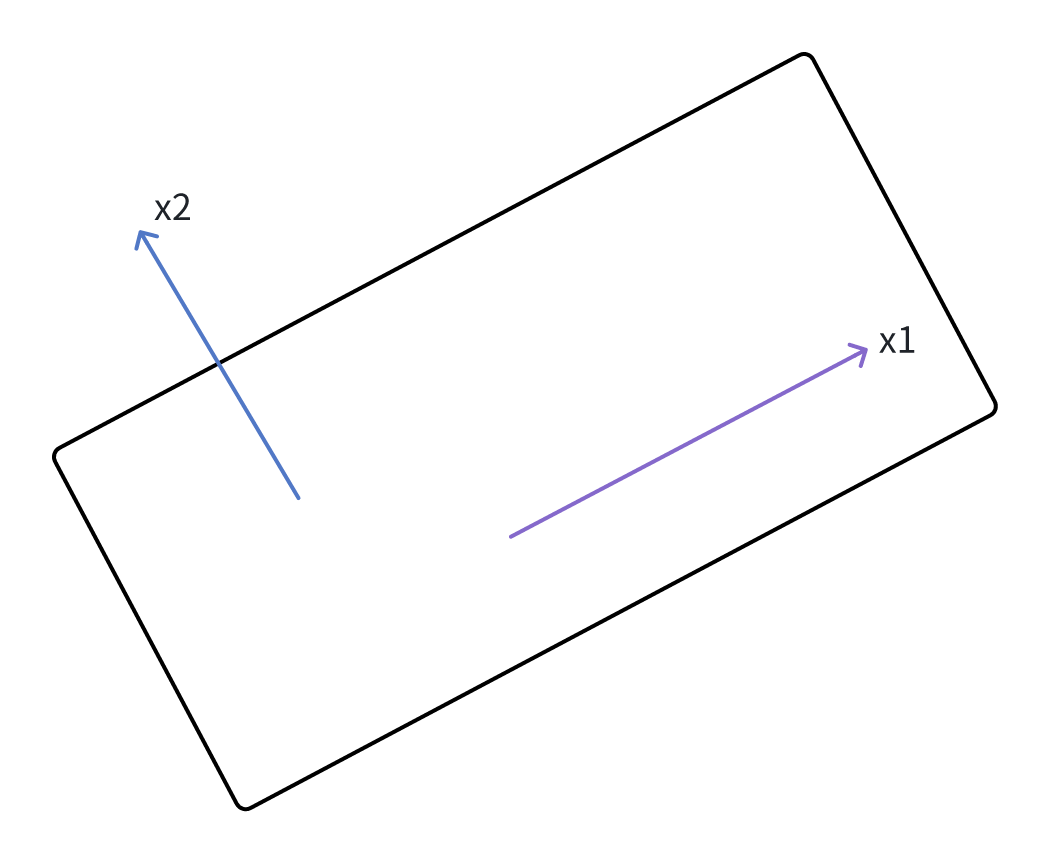
我们取较为特殊的向量：

(1) 如果对任意平面上的$x_1$来说，投影矩阵根本不会影响它的大小，所以就有：$Ax_1 = x_1$恒成立。此时得到一个 λ：1。

(2) 如果对垂直于平面的任意$x_2$来说，投影矩阵作用在此向量之后始终会有：$Ax_2 = 0$恒成立。如此即得到第二个 λ：0。

2.2 求解方法

接下来我们给出特征值、特征向量的一般求解方法。我们对方程进行一些处理：

$$Ax=\lambda x \to (A - \lambda I)x = 0$$

即$(A - \lambda I)$是不可逆矩阵 $\to A - \lambda I$行列式为 0

如上即为求解特征值的步骤。n 阶一共应该有 n 个特征值。

求解特征向量只需要取求解出的一个特征值 λ，此时$A - \lambda I$是一个不可逆矩阵，利用$(A - \lambda I)X = 0$求解零空间中的向量即为矩阵的特征向量。

【例 1】求矩阵$\begin{bmatrix}3 & 1\\1 & 3\end{bmatrix}$的特征向量与特征值。

沿袭我们上述思路，构造矩阵$\begin{bmatrix}3 - \lambda & 1\\1 & 3 - \lambda\end{bmatrix}$。求解行列式 = 0 即可。解得两个特征值：$\lambda_1 = 2$，$\lambda_2 = 4$ 。

求解特征向量：直接代入特征值消元。

$$A - 4I=\begin{bmatrix}-1 & 1\\1 & -1\end{bmatrix}$$

即：$\begin{bmatrix}-1 & 1\\1 & -1\end{bmatrix}X = 0$，解得$x_1=\begin{bmatrix}1\\1\end{bmatrix}$

$$A - 2I=\begin{bmatrix}1 & 1\\1 & 1\end{bmatrix}$$

即：$\begin{bmatrix}1 & 1\\1 & 1\end{bmatrix}x = 0$，解得$x_2=\begin{bmatrix}-1\\1\end{bmatrix}$

注：在这里注意一点，我们很容易发现：$\lambda_1+\lambda_2 = 6$，正好是$\begin{bmatrix}3 & 1\\1 & 3\end{bmatrix}$对角线上元素的和，称为“迹”。特征值之和与迹相等，这也是一个重要的定理。而且又有$\lambda_1\lambda_2 = 8$，即为行列式$\begin{bmatrix}3 & 1\\1 & 3\end{bmatrix}$的值，这也是一个普遍规律，特征值之积为 A 矩阵行列式的值。

【例 2】在例 1 的基础上，如果矩阵$A=\begin{bmatrix}3 & 1\\1 & 3\end{bmatrix}+3I$，那么它的特征值、特征向量将如何变化？

首先，列出这部分核心的等式：$Ax=\lambda x$，则根据题意，改变后的方程变为：$(A + 3I)x=\lambda x+3x=(\lambda + 3)x$。也就是说，新的特征值变为$\lambda + 3$，而对应的特征向量不会改变，因为等式两边同等的有 $3Ix$与$3x$，不会影响特征向量的值。

2.3 特殊情况说明

我们通过两个例题说明下这部分求解中可能遇到的特殊情况。

【例 3】旋转矩阵 Q 使得每个向量旋转 90°，记$Q=\begin{bmatrix}0 & -1\\1 & 0\end{bmatrix}$（$\begin{bmatrix}\cos90^{\circ} & -\sin90^{\circ}\\\sin90^{\circ} & \cos90^{\circ}\end{bmatrix}$），求解特征值与特征向量。

思路：

这个问题我们如果从迹与 A 行列式的角度分析，得到：$\lambda_1\lambda_2 = 1$

$$\lambda_1+\lambda_2 = 0$$

这样特征值不存在么？我们换一种思路：使用$Qx=\lambda x$这个式子，化简求解$Q-\lambda_i$的行列式的值，使其为 0。得到$\lambda^2 + 1 = 0$，解得 λ 为虚数：i 与-i。代入之前的方程，完全满足。

启示：我们发现 Q 是反对称矩阵$(A^T = -A)$，而我们之前求的都是对称矩阵的特征值，也就是说，对称矩阵的特征值为实数，而反对称矩阵的特征值为虚数，这是两个极端。

【例 4】$A=\begin{bmatrix}3 & 1\\0 & 3\end{bmatrix}$，求特征值与特征向量。

思路：

这是个上三角矩阵，求解$A-\lambda I$行列式时会发现，$\lambda_1=\lambda_2 = 3$，这时的特征向量只会有一个，也就是说，三角矩阵的结构的特殊性导致了其行列式为对角线上元素，而如果对角线上两个元素相等，那么就会造成特征向量短缺情况。

三、学习感悟

本节内容不是很困难，重点在于特征值与特征向量的求解，其实只要使用$A-\lambda x$（这里应该是$A - \lambda I$）求解就没错，特别注意一下虚数情况就好了。重点是理解特征值如何求解以及特征值到底代表着什么。