Linear Algebra-克莱姆法则、逆矩阵、体积-20

一、知识概述

上一节我们系统学习了行列式的计算方法，本节课将聚焦于行列式的三大核心应用：克莱姆法则、逆矩阵公式以及体积计算。这些内容将帮助我们从更本质的角度理解行列式的几何意义与代数价值。

二、逆矩阵公式

公式定义

对于可逆矩阵 $A$ ，其逆矩阵可表示为：

A^{- 1} = \frac{1}{| A |} C^{T}

其中 $C$ 是由代数余子式构成的矩阵， $C^{T}$ 称为伴随矩阵。

其中 $A^{- 1}$ 是 $m \times n$ 的矩阵， $| A |$ 是 n 个元素的乘积， $C^{T}$ 中各元素由 $n - 1$ 个乘积组成。

二阶矩阵示例

{[\begin{matrix} a & b \\ c & d \end{matrix}]}^{- 1} = \frac{1}{a d - b c} [\begin{matrix} d & - b \\ - c & a \end{matrix}]

公式验证

通过矩阵乘法验证公式正确性：

A \cdot A^{- 1} = A \cdot \frac{1}{| A |} C^{T} = I

展开乘积矩阵 $A C^{T}$ ：

A C^{T} = [\begin{array}{ccc} a_{11} & . . . & a_{1 n} \\ . . . & . . . & . . . \\ a_{n 1} & . . . & a_{n n} \end{array}] [\begin{array}{ccc} C_{11} & . . . & C_{n 1} \\ . . . & . . . & . . . \\ C_{1 n} & . . . & C_{n n} \end{array}] = [\begin{array}{ccc} | A | & 0 & 0 \\ 0 & . . . & 0 \\ 0 & 0 & | A | \end{array}] = | A | [\begin{array}{ccc} 1 & 0 & 0 \\ 0 & . . . & 0 \\ 0 & 0 & 1 \end{array}] = | A | I

这里有一个问题,那第一行为例,为什么 $[\begin{array}{llll} a_{11} & a_{12} & . . . & a_{1 n} \end{array}]$ 这个行向量在和不属于这行元素的代数余子式构成的列向量相乘时,得到的结果为零呢?也就是为什么 $[\begin{array}{ccc} | A | & 0 & 0 \\ 0 & . . . & 0 \\ 0 & 0 & | A | \end{array}]$ 中除对角线外,其余元素都为零呢?

很简单,就以 A 的第一行和 $C^{T}$ 的第二列为例:

[\begin{array}{llll} a_{11} & a_{12} & . . . & a_{1 n} \end{array}] [\begin{matrix} C_{21} \\ C_{22} \\ . . . \\ C_{2 n} \end{matrix}] = a_{11} C_{21} + a_{12} C_{22} + \dots + a_{1 n} C_{2 n}

我们构造一个新矩阵来表现这个结果:

[\begin{array}{cccc} a_{11} & a_{12} & . . . & a_{1 n} \\ a_{11} & a_{12} & . . . & a_{1 n} \\ a_{31} & a_{32} & . . . & a_{3 n} \\ . . . & . . . & . . . & . . . \\ a_{n 1} & a_{n 2} & . . . & a_{n n} \end{array}]

这个矩阵前两行相同,将这个矩阵按第二行展开求行列式,即为:

| \begin{array}{cccc} a_{11} & a_{12} & \dots & a_{1 n} \\ a_{11} & a_{12} & \dots & a_{1 n} \\ a_{31} & a_{32} & \dots & a_{3 n} \\ . . . & . . . & . . . & . . . \\ a_{n 1} & a_{n 2} & . . . & a_{n n} \end{array} | = a_{11} C_{21} + a_{12} C_{22} + \dots + a_{1 n} C_{2 n}

同时,由于这个矩阵前两行相同,故其行列式为 0｡这样就得到了:

a_{11} C_{21} + a_{12} C_{22} + \dots + a_{1 n} C_{2 n} = 0

其余位置以此类推,所以 $[\begin{array}{ccc} | A | & 0 & 0 \\ 0 & . . . & 0 \\ 0 & 0 & | A | \end{array}]$ 中除对角线,其余位置均为 0｡

构造两行相同的矩阵，其行列式为零，从而推导出：

a_{i 1} C_{j 1} + a_{i 2} C_{j 2} + \dots + a_{i n} C_{j n} = 0 (i \neq j)

逆矩阵公式帮助我们了解了另一种原矩阵与逆矩阵之间的关系,可以理解原矩阵的变化对逆矩阵的影响｡

三、克莱姆法则

基于上面的逆矩阵公式，我们可以找到另一种寻找方程的解的方式，也就是由可逆矩阵 A 构成的方程 $A x = b$ ，这里不用消元法来解：

x = A^{- 1} b = \frac{1}{| A |} C^{T} b

基本不用，作了解即可

四、体积计算

直接给出应用:行列式的值是一个六面体的体积｡

矩阵 $A = [\begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{matrix}]$ 的行列式绝对值表示由其列向量张成的平行六面体体积：

体积 = | det (A) |

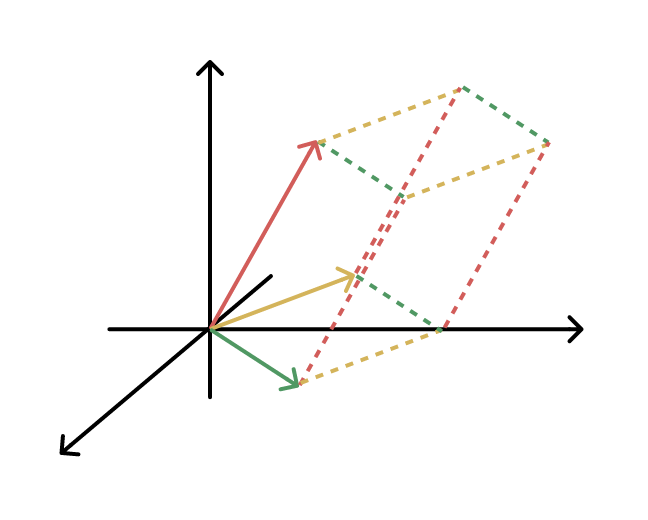
行列式的值有正负，所以该六面体的体积即为行列式的绝对值。而正负号的作用是告诉我们这个立体是左手系的还是右手系的。因为当我们调换这个立体的两条边之后,我们得到的会是不同系下的立体，其体积不会变，但是旋转顺序变了。研究几个特别的矩阵：

单位矩阵：对应边长为 1 的标准立方体。
正交矩阵：还记得我们之前介绍的正交阵 Q,它除了正交这个性质之外,还有一点,即各向量长度均为 1。 $(Q^{T} Q = I)$ ｡所以 Q 构成的立体也是三个边长为 1 的立方体,只是体现在坐标中时与单位矩阵对应的立体位置不同，可能旋转或反射。

五、学习总结

逆矩阵公式揭示了矩阵与其伴随矩阵的深刻联系，为理论分析提供了重要工具。
克莱姆法则通过行列式表达解的结构，但计算效率低于消元法，仅适合理论推导。
体积解释赋予行列式直观的几何意义，将代数运算与空间度量统一起来。

建议重点掌握逆矩阵公式的推导逻辑和体积计算的几何应用，克莱姆法则可作为行列式性质的综合演练。