Linear Algebra-正交矩阵、Gram-Schmidt 正交化和QR分解-17

一、知识概要

本节以上一节结尾介绍的标准正交向量为切入点，重点阐述标准正交向量组的性质与优势，同时详细讲解将一组向量化为标准正交向量组的方法——Gram - Schmidt 正交化。

二、标准正交向量

2.1 回顾标准正交向量

上节介绍过标准正交向量，我们借助一个式子来回顾其性质。设 $q$ 是标准正交向量组中的任意向量，对于向量组中的向量 $q_i$ 和 $q_j$ ，有：

$q_{i}^{T}q_{j}=\begin{cases}0 & (i\neq j) \\ 1 & (i = j)\end{cases}$

这个式子清晰地展现了标准正交向量组内各向量的性质。其中，“标准”意味着向量的长度为 1，即向量是单位向量；“正交”表示不同向量之间的内积为 0 ，也就是相互垂直。

2.2 标准正交矩阵 Q

定义：这节引入了标准正交矩阵 $Q$ 的概念。标准正交矩阵 $Q$ 是将标准正交向量组中的 $q_1,q_2,\cdots,q_n$ 按列排列在同一个矩阵中，即：

$Q=\begin{bmatrix}q_1&\cdots&q_n\\\vdots&\ddots&\vdots\\\vdots&&\vdots\end{bmatrix}$

性质：标准正交矩阵具有一个重要性质，即 $Q^{T}Q$ 的计算结果为单位矩阵 $I$ 。计算过程如下：

$Q^{T}Q=\begin{bmatrix}q_1\\q_2\\\vdots\\q_n\end{bmatrix}\begin{bmatrix}q_1&q_2&\cdots&q_n\end{bmatrix}=\begin{bmatrix}1&0&\cdots&0&0\\0&1&\cdots&0&0\\\vdots&\vdots&\ddots&\vdots&\vdots\\0&0&\cdots&1&0\\0&0&\cdots&0&1\end{bmatrix}=I$

特别地，当 $Q$ 是方阵时，我们把这样的矩阵称为正交矩阵。这是因为方阵存在逆矩阵，由 $Q^{T}Q = I$ ，可以直接得出 $Q$ 的逆矩阵 $Q^{-1}=Q^{T}$ 。

例如，对于矩阵 $Q=\begin{bmatrix}0&0&1\\1&0&0\\0&1&0\end{bmatrix}$ ，其转置 $Q^{T}=\begin{bmatrix}0&1&0\\0&0&1\\1&0&0\end{bmatrix}$ ，同时也是它的逆矩阵 $Q^{-1}$ ，且满足 $QQ^{T}=\begin{bmatrix}0&0&1\\1&0&0\\0&1&0\end{bmatrix}\begin{bmatrix}0&1&0\\0&0&1\\1&0&0\end{bmatrix}=I$ 。

再如，根据之前介绍的正交向量组 $\begin{bmatrix}\cos\theta\\\sin\theta\end{bmatrix}$ ， $\begin{bmatrix}-\sin\theta\\\cos\theta\end{bmatrix}$ ，写成矩阵形式为 $Q=\begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{bmatrix}$ ，这也是一个正交矩阵。

需要注意的是，在构建正交矩阵时，不要忘记对向量进行单位化。例如，矩阵 $\begin{bmatrix}1&1\\1& - 1\end{bmatrix}$ 各列是正交的，但不是正交矩阵，因为没有单位化。正确的正交矩阵应该是 $\frac{1}{\sqrt{2}}\begin{bmatrix}1&1\\1& - 1\end{bmatrix}$ 。由这个矩阵还可以延伸出阿达马矩阵，这里暂不详细介绍。

此外，标准正交矩阵不会改变向量的长度，即对于任意向量 $x$ ， $||Qx||=||x||$ ，因为 $(Qx)^T(Qx)=x^TQ^TQx=x^TIx=x^Tx$ 。

2.3 标准正交矩阵的作用

标准正交矩阵具有诸多优良性质，下面介绍它在投影矩阵和拟合方程方面的应用。

投影矩阵：我们知道投影矩阵的一般公式为 $P = A(A^{T}A)^{-1}A^{T}$ 。当取的 $A$ 矩阵是标准正交矩阵 $Q$ 时，投影矩阵变为 $Q(Q^{T}Q)^{-1}Q^{T}$ 。由于 $Q^{T}Q = I$ ，所以 $Q(Q^{T}Q)^{-1}Q^{T}=QQ^{T}$ 。

特别地，当 $Q$ 是方阵（即正交阵）时，因为 $Q^{T}=Q^{-1}$ ，此时投影矩阵 $P = QQ^{T}=I$ 。将其代入投影矩阵的两条性质（投影矩阵为对称矩阵，且 $P^{2}=P$ ）进行验证：

对称性： $(QQ^{T})^{T}=(Q^{T})^{T}Q^{T}=QQ^{T}$ ，所以 $QQ^{T}$ 是对称矩阵。
$P^{2}$ 性质： $(QQ^{T})^{2}=QQ^{T}QQ^{T}=Q(Q^{T}Q)Q^{T}=QQ^{T}=P$ 。

拟合方程：之前介绍的拟合方程为 $A^{T}b = A^{T}A\hat{x}$ 。当使用标准正交基，即 $A = Q$ 为标准正交矩阵时，方程可化简为：

$Q^{T}Q\hat{x}=Q^{T}b$

因为 $Q^{T}Q = I$ ，所以进一步得到：

$I\hat{x}=Q^{T}b$

即 $\hat{x}=Q^{T}b$ ，展开为分量形式为 $\hat{x}_{i}=q_{i}^{T}b$ 。这表明，如果已知标准正交基，那么向量 $b$ 在第 $i$ 个基上的投影就是对应基向量 $q_{i}^{T}b$ 。

由此可见，当选择标准正交向量作为基时，投影矩阵相关公式中的 $A$ 都可以替换为 $Q$ ，这使得很多公式得到简化，计算更加便捷。

三、Gram - Schmidt 正交化

这部分介绍一种方法，能够从线性无关向量组出发，将其矩阵标准正交化。

二维向量示例：假设有两个线性无关的向量 $a$ ， $b$ ，我们希望得到标准正交向量 $q_1$ ， $q_2$ 。也可以理解为，空间原来的两个基 $a$ ， $b$ 不满足标准正交条件，现在通过 Gram - Schmidt 正交化并单位化，将它们变为两个标准正交基 $q_1$ ， $q_2$ 。
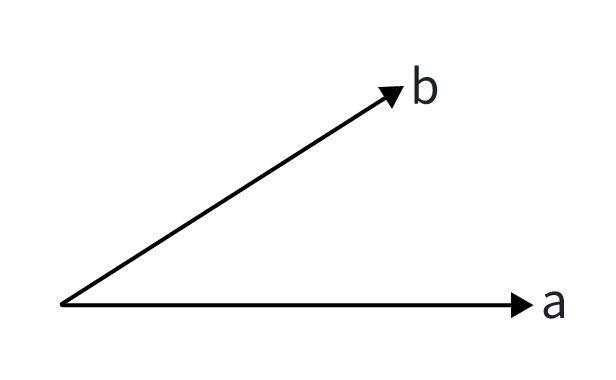
- 首先假设已知一组正交基 $A$ ， $B$ ，那么 $q_1=\frac{A}{\vert A\vert}$ ， $q_2=\frac{B}{\vert B\vert}$ 。所以关键在于找到两个正交的基。
- 以向量 $a$ ， $b$ 为例，它们线性无关意味着不共线。将 $a$ 向量定为 $A$ 向量，然后把 $b$ 向量投影到 $a$ 向量上。
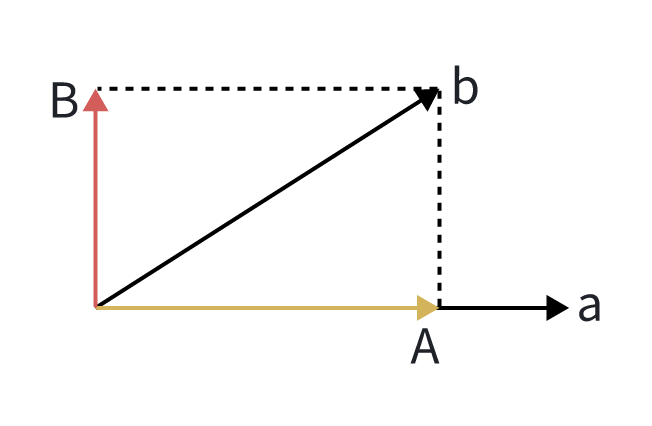
- 取投影垂线所在直线的正方向为另一个基向量 $B$ 的方向，投影垂线长度为 $B$ 的长度。根据投影知识， $B$ 的表达式为：

$B = b-A(A^{T}A)^{-1}A^{T}b$

对上式进行检验，计算 $A^{T}B$ ：

$A^{T}B=A^{T}(b - A(A^{T}A)^{-1}A^{T}b)=A^{T}b-{A^{T}A}(A^{T}A)^{-1}A^{T}b=A^{T}b - A^{T}b = 0$

这说明 $A$ 与 $B$ 是正交的。然后通过 $q_1=\frac{A}{\vert A\vert}$ ， $q_2=\frac{B}{\vert B\vert}$ 对各个向量进行单位化，就得到了与 $a$ ， $b$ 同空间的标准正交基 $q_1$ ， $q_2$ 。

三维向量推广：对于三维向量，寻找三个正交的向量 $A$ ， $B$ ， $C$ ，其中 $A$ ， $B$ 的确定方法与二维类似：

$A = a$ $B = b-A(A^{T}A)^{-1}A^{T}b$

而向量 $C$ 通过将 $c$ 减去在 $A$ ， $B$ 上的投影得到：

$C = c-A(A^{T}A)^{-1}A^{T}c-B(B^{T}B)^{-1}B^{T}c$

得到三个正交的向量 $A$ ， $B$ ， $C$ 后，再进行单位化即可得到标准正交向量组。

具体例题：已知 $a=\begin{bmatrix}1\\1\\1\end{bmatrix}$ ， $b=\begin{bmatrix}1\\0\\2\end{bmatrix}$ ，求标准正交矩阵 $Q$ 。

首先，令 $A = a=\begin{bmatrix}1\\1\\1\end{bmatrix}$ 。
计算 $B$ ：

$B = b-A(A^{T}A)^{-1}A^{T}b=\begin{bmatrix}1\\0\\2\end{bmatrix}-\frac{1\times1 + 1\times0 + 1\times2}{1\times1 + 1\times1 + 1\times1}\begin{bmatrix}1\\1\\1\end{bmatrix}=\begin{bmatrix}1\\0\\2\end{bmatrix}-\begin{bmatrix}1\\1\\1\end{bmatrix}=\begin{bmatrix}0\\ - 1\\1\end{bmatrix}$

1	- 对$$A$$，$$B$$进行单位化，得到标准正交矩阵$$Q$$：

$Q=\begin{bmatrix}q_1&q_2\end{bmatrix}=\begin{bmatrix}\frac{1}{\sqrt{3}}&0\\\frac{1}{\sqrt{3}}&-\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{3}}&\frac{1}{\sqrt{2}}\end{bmatrix}$

从矩阵角度分析：原始矩阵 $A=\begin{bmatrix}1&1\\1&0\\1&2\end{bmatrix}$ ，经过 Gram - Schmidt 正交化后得到 $Q=\begin{bmatrix}\frac{1}{\sqrt{3}}&0\\\frac{1}{\sqrt{3}}&-\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{3}}&\frac{1}{\sqrt{2}}\end{bmatrix}$ 。观察两个矩阵的列空间，会发现它们是相同的。这意味着正交化过程是在同一个空间中进行的，只是最终得到了一个更优的标准正交基。

从矩阵分解的角度看，类似于 $A$ 的 $LU$ 分解，在 Gram - Schmidt 正交化中， $A$ 可分解为 $Q$ 与 $R$ ，其中 $R$ 是上三角矩阵：

$A = QR$

其中， $A=\begin{bmatrix}a_1&a_2\end{bmatrix}$ （原始向量，如 $a$ ， $b$ ， $c$ 等）， $Q=\begin{bmatrix}q_1&q_2\end{bmatrix}$ （标准正交基 $q_1$ ， $q_2$ ）， $R=\begin{bmatrix}a_1^{T}q_1&a_2^{T}q_1\\a_1^{T}q_2&a_2^{T}q_2\end{bmatrix}$ 。

在这个例子中， $R$ 中的 $a_1^{T}q_2$ 为 0 。这是因为 $a_1$ 是 $A$ 方向上的向量， $q_2$ 是 $B$ 方向上的向量， $A$ 与 $B$ 正交，所以它们的内积为 0 。其他情况类似，这是 Gram - Schmidt 正交化的一个重要性质。

$R$ 在 $Q$ 右侧相当于对 $Q$ 做列操作，即 $A$ 的列向量是 $Q$ 列向量的线性组合，而 $Q$ 为 $A$ 列空间的一组标准正交基，则 $R$ 的元素实际上是 $A$ 的列向量基于 $Q$ 这组标准正交基的权值。

采用矩阵的 QR 分解来帮助求解 Ax=b 的问题，最大的优势是提高了数值的稳定性。

QR 分解在最小二乘法中的应用

由前文可知，最小二乘法的结果为 $A^TA\hat{x}=A^Tb$ ，又利用 $A$ 的 QR 分解结果可知， $A^TA=(QR)^TQR=R^TQ^TQR=R^TR$ ，因此最小二乘的结果 $A^TA\hat{x}=A^Tb$ 可以化简为 $R^TR\hat{x}=R^TQ^Tb$ ，最后我们得到了 $R\hat{x}=Q^Tb$ ，这个结果对我们而言很友好。

与直接求解 $Ax=b$ 而言，我们通过回代法求解 $R\hat{x}=Q^Tb$ 可以很快，计算代价就是 Gram-Schmidt 正交化的计算过程，也就是需要构造出正交矩阵 $Q$ 和上三角矩阵 $R$ ，使得 $A=Q(orthogonal)R(triangular)$ 。