Linear Algebra-求解 Ax=0，主变量，特解-07

概要

记得上一节中我们讨论了列空间和零空间的相关问题，那么这一节我们从它们的定义过渡到它们的计算，即如何求解出这些空间的一般形式。给出一种可以解出 $Ax=0$ 中的 x 构成的零空间的算法。

消元法求解零空间

记得之前在讲解使用消元法解方程组 $Ax=b$ 时，我们对一种情况是无法处理的，那就是矩阵 A 不可逆的情况。之前对这种情况的解释是：求出的解不唯一。这正好对应了我们现在学到的“空间”概念。

我们首先从最简单的零空间(b=0)的计算谈起。

消元法确定主变量与自由变量(消元)

【例】设 $A=\begin{bmatrix} 1 & 2 & 2 & 2\\ 2 & 4 & 6 & 8\\ 3 & 6 & 8 & 10\\ \end{bmatrix}$ ，求由 Ax=0 中的 x 构成的零空间。

Ax=0 其实就是一个方程组：

$\begin{bmatrix} 1 & 2 & 2 & 2\\ 2 & 4 & 6 & 8\\ 3 & 6 & 8 & 10\\ \end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4\\ \end{bmatrix}=0$

还是之前学过的消元法来直接处理矩阵 A：

$\begin{bmatrix} 1 & 2 & 2 & 2\\ 2 & 4 & 6 & 8\\ 3 & 6 & 8 & 10\\ \end{bmatrix}->\begin{bmatrix} 1 & 2 & 2 & 2\\ 0 & 0 & 2 & 4\\ 0 & 0 & 2 & 4\\ \end{bmatrix}->\begin{bmatrix} 1 & 2 & 2 & 2\\ 0 & 0 & 2 & 4\\ 0 & 0 & 0 & 0\\ \end{bmatrix}=U$

首先注意 A 矩阵消元之后只有两个主元：1 和 2，主元的个数被称为秩，即 A 的秩为 2。

接下来应该是进行回代求解了，但是在这之前，由于消元得到的 U 不是一个严格的上三角矩阵，因此方程的解就不唯一，所以先来明确几个概念。

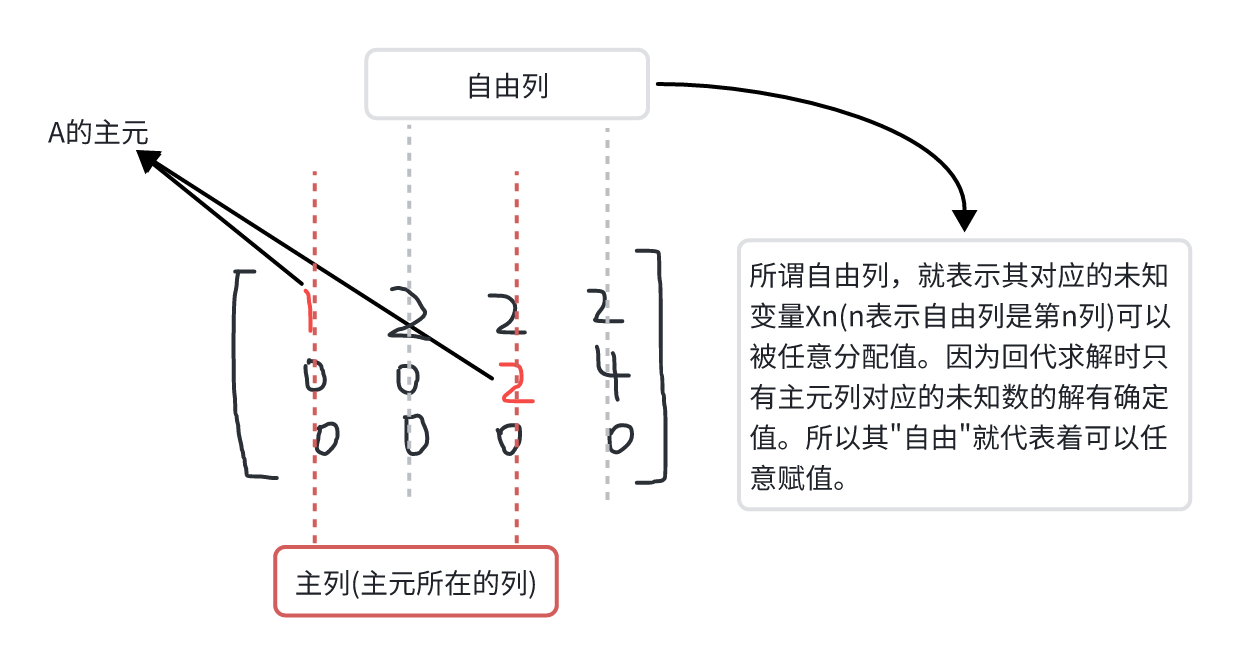
Linear_Algebra70

所以这个 U 的主变量(主元)为 $x_1,x_3$ 。自由变量为 $x_2,x_4$ 。

对自由变量赋值覆盖零空间(回代)

首先给自由变量 $\begin{bmatrix} x_2\\ x_4\\ \end{bmatrix}$ 赋值为 $\begin{bmatrix} 1\\ 0\\ \end{bmatrix}$ 。

回代入方程组：

$x_1+2x_2+2x_3+2x_4=0\\2x_3+4x_4=0$

当 $\begin{bmatrix} x_2\\ x_4\\ \end{bmatrix}=\begin{bmatrix} 1\\ 0\\ \end{bmatrix}$ 时，解向量为： $\begin{bmatrix} -2\\ 1\\ 0\\ 0\\ \end{bmatrix}$ 。

再给自由变量 $\begin{bmatrix} x_2\\ x_4\\ \end{bmatrix}$ 赋值为 $\begin{bmatrix} 0\\ 1\\ \end{bmatrix}$ 。

再次回代入方程组，此时的解向量为 $\begin{bmatrix} 2\\ 0\\ -2\\ 1\\ \end{bmatrix}$ 。

还有别的给 $\begin{bmatrix} x_2\\ x_4\\ \end{bmatrix}$ 赋值的方法吗？很明显其余的赋值方法都可以被 $\begin{bmatrix} 1\\ 0\\ \end{bmatrix}$ 和 $\begin{bmatrix} 0\\ 1\\ \end{bmatrix}$ 的线性组合所覆盖，所以这两个解向量足够代表零空间的特征了，我们称这两个解向量为：特解。其特殊之处便在于给自由变量赋值为了 $\begin{bmatrix} 1\\ 0\\ \end{bmatrix}$ 和 $\begin{bmatrix} 0\\ 1\\ \end{bmatrix}$ 。

通过特解的任意倍的线性组合可以构造出整个零空间。

即 $Ax=0$ 的所有解，或者说 $Ax=0$ 中的 x 构成的零向量空间为：

$x=c\begin{bmatrix} -2\\ 1\\ 0\\ 0\\ \end{bmatrix}+d\begin{bmatrix} 2\\ 0\\ -2\\ 1\\ \end{bmatrix}$

算法总结

对于一个 $m\times n$ 的矩阵 A，若其秩(R)为 r，那么就意味着其主变量为 r 个，而自由变量为 n-r 个。也就是只有 r 个方程起作用，而一共有 n 个变量 x，我们将其中的 n-r 个自由变量依次赋值为： $\begin{bmatrix} 1\\ 0\\ ...\\ 0\\ \end{bmatrix},\begin{bmatrix} 0\\ 1\\ ...\\ 0\\ \end{bmatrix},...,\begin{bmatrix} 0\\ 0\\ ...\\ 1\\ \end{bmatrix}$ 。接下来解方程求特解，将特解的任意倍进行线性组合就可以了。

简化行阶梯形式

上面的消元法看上去已经很完美了，但是最后一步解方程还有化简的余地，最后得到的 U 矩阵还可以被进一步化简。

拿上面【例】中的 U 矩阵 $\begin{bmatrix} 1 & 2 & 2 & 2\\ 0 & 0 & 2 & 4\\ 0 & 0 & 0 & 0\\ \end{bmatrix}$ 为例，继续化简：

首先向上消元，使主元列除主元之外都是 0： $\begin{bmatrix} 1 & 2 & 0 & -2\\ 0 & 0 & 2 & 4\\ 0 & 0 & 0 & 0\\ \end{bmatrix}$
提出一列元素公倍数，使主元均为 1： $R=2\begin{bmatrix} 1 & 2 & 0 & -2\\ 0 & 0 & 1 & 2\\ 0 & 0 & 0 & 0\\ \end{bmatrix}$
列交换，使左上角变为单位阵 I： $2\begin{bmatrix} 1 & 0 & 2 & -2\\ 0 & 1 & 0 & 2\\ 0 & 0 & 0 & 0\\ \end{bmatrix}$

在矩阵中主元行和主元列的交汇处存在一个单位阵，通过“列交换”，可以将矩阵 R 中的主元列集中在左侧，从而在左上角形成这个单位阵，而将自由列集中在矩阵的右侧。如果矩阵 A 中的某些行是线性相关的，则在矩阵 R 的下半部分就会出现一些完全为 0 的行向量。

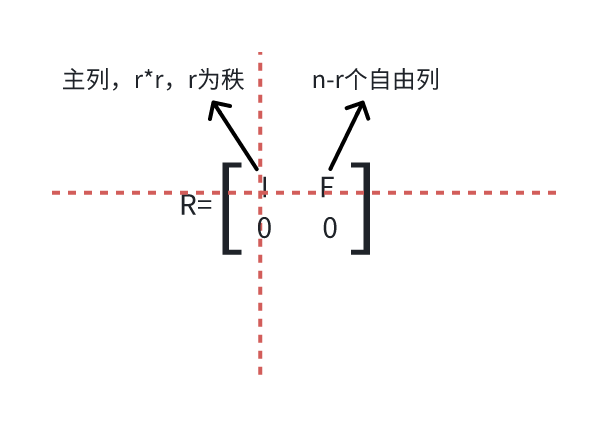
Linear_Algebra71

这里的 $I$ 是一个 $r\times r$ 的方阵，F 即自由列消元后组成的部分。

原方程 $Ax=0$ 变为求解 R 的主元行乘以 x， $\begin{bmatrix} I & F \end{bmatrix}\begin{bmatrix} x_{pivot} \\ x_{free} \end{bmatrix}=0$

我们将 $Ax=0$ 的特解作为列向量写成矩阵 $N$ ，即零空间矩阵。则其形式为 $N=\begin{bmatrix} \\ I \end{bmatrix}$ 。这里的I为一个 $(n-r)\times (n-r)$ 的矩阵，就是对n-r个自由变量分别赋值1所构造出来的，零空间矩阵满足 $RN=0$ ，这里的0是一个 $m\times (n-r)$ 的矩阵，则从矩阵分块乘法运算可知零空间矩阵上半部分为 $-F$ ，即N的最终形式为 $N=\begin{bmatrix} -F\\ I \end{bmatrix}$ 。