Linear Algebra-列空间和零空间-06

概要

本节从之前学习的子空间开始，介绍了子空间的部分性质。并重点介绍了列空间与方程 $Ax=b$ 之间的联系，并由此引出了零空间，根据 $Ax=b$ 这个方程给出了两种构建子空间的方法。

子空间

子空间回顾

首先我们回顾一下上次讲到的子空间。首先明确，子空间必须对线性运算封闭。我们从一个简单的向量空间： $R^3$ 空间开始。其图像如下，整个三维空间皆为 $R^3$ 空间。

three_dimension

上一节中我们学习过， $R^3$ 的子空间就是如下三个（注：子空间必须包含原点，即零向量）：

穿过原点的无限延伸的平面 P；
穿过原点的无限延伸的直线 L；
Z，原点；

反映在图像上，即：

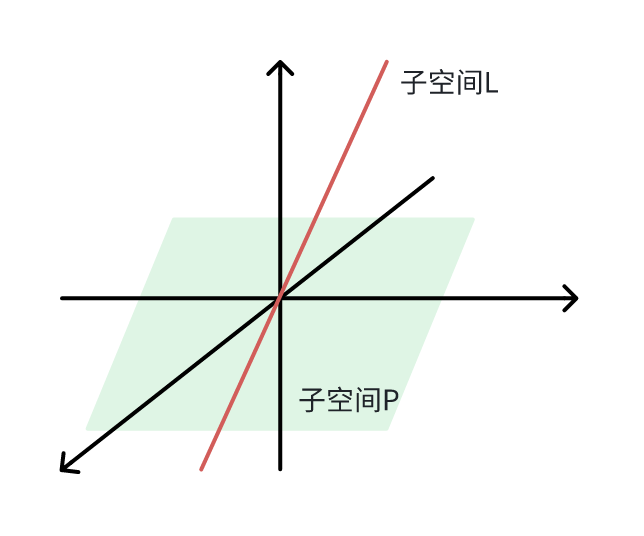
liekongjian1

很明显，子空间直线 L 或平面 P 上，任取两个向量相加，得到的向量仍在该子空间中。而且将其上的向量做数乘伸长或缩短一定倍数，其结果也还在该子空间中，所以它们都对线性运算封闭。

子空间的“交”与“并”

上面我们都是分别研究的两个子空间，那么接下来我们对两个空间之间联系的部分展开讨论。

P∪L 空间

我们还是聚焦于 $R^3$ 的子空间 P 与 L，首先要研究的就是他们的并空间，即：现有一集合，包含了 P 与 L 中的所有向量，那么这个集合是子空间吗？

答案是否定的。

很明显，我们将直线 L 与平面 P 看做同一个集合 P∪L 之后，这个集合对线性运算并不封闭。比如我们随便在直线 L 上取一个向量 a，在平面 P 上取一个向量 b，此时向量 a+b 的方向就会夹在直线 L 与平面 P 之间，脱离了 P∪L 的范围，因此 P∪L 无法构成子空间。

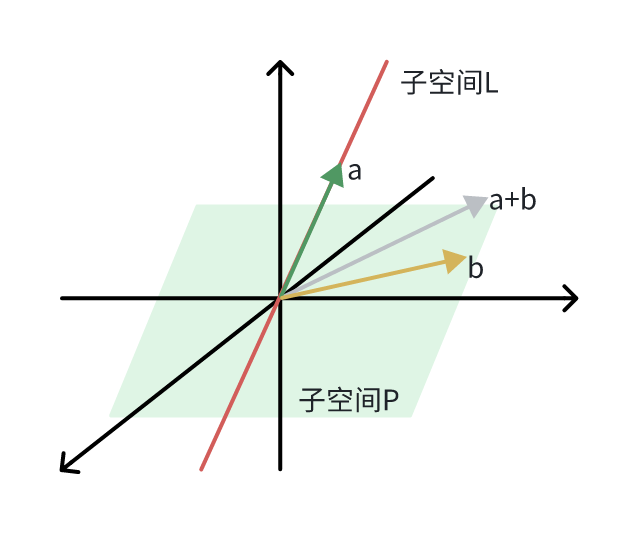
liekongjian2

P∩L 空间

如果看的是两个子空间的交集，那么上面那个 $R^3$ 的例子就很合适。因为平面 P 与直线 L 只在原点相交，而原点显然是 $R^3$ 的子空间之一。

如果推广到任意两个子空间的交呢？假设现在有子空间 S 和 T，问其交集 S∩T 是否为子空间？

这次答案是肯定的。

为什么呢？抽象层面上来看，S∩T 的集合是比 S，T 限制条件更多的集合，相当于一个更小的集合，所以 S∩T 势必满足原本 S 和 T 的条件，所以可以构成一个子空间。

列空间

列空间回顾

我们通过一个例子来回顾之前的内容。

现有矩阵 $A=\begin{bmatrix} 1 & 1 & 2\\ 2 & 1 & 3\\ 3 & 1 & 4\\ 4 & 1 & 5\\ \end{bmatrix}$ ，矩阵的列向量 $\begin{bmatrix} 1\\ 2\\ 3\\ 4\\ \end{bmatrix}\begin{bmatrix} 1\\ 1\\ 1\\ 1\\ \end{bmatrix} \begin{bmatrix} 2\\ 3\\ 4\\ 5\\ \end{bmatrix}$ 均是 $R^4$ 中的四维向量，所以A的列空间是 $R^4$ 的子空间。

那么列空间里包含了什么呢？除了 $\begin{bmatrix} 1\\ 2\\ 3\\ 4\\ \end{bmatrix}\begin{bmatrix} 1\\ 1\\ 1\\ 1\\ \end{bmatrix} \begin{bmatrix} 2\\ 3\\ 4\\ 5\\ \end{bmatrix}$ 三个列向量，列空间里还包含着它们的各种线性组合。也就是说，A的列空间是由 $\begin{bmatrix} 1\\ 2\\ 3\\ 4\\ \end{bmatrix}\begin{bmatrix} 1\\ 1\\ 1\\ 1\\ \end{bmatrix} \begin{bmatrix} 2\\ 3\\ 4\\ 5\\ \end{bmatrix}$ 三个列向量张开的一个子空间。

那么这个子空间有多大呢？这就需要 $Ax=b$ 方程来解释了。

Ax=b 的空间解释

还是取 $A=\begin{bmatrix} 1 & 1 & 2\\ 2 & 1 & 3\\ 3 & 1 & 4\\ 4 & 1 & 5\\ \end{bmatrix}$ 。假设有一个方程 $Ax=b$ 如下：

$Ax=\begin{bmatrix} 1 & 1 & 2\\ 2 & 1 & 3\\ 3 & 1 & 4\\ 4 & 1 & 5\\ \end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ x_3\\ \end{bmatrix}=\begin{bmatrix} b_1\\ b_2\\ b_3\\ b_4\\ \end{bmatrix}=b$

首先第一个问题：这个方程是否始终有解？

我们看到，Ax 的本质就是对 A 的列向量进行线性组合：

$Ax=\begin{bmatrix} 1 & 1 & 2\\ 2 & 1 & 3\\ 3 & 1 & 4\\ 4 & 1 & 5\\ \end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ x_3\\ \end{bmatrix}=x_1\begin{bmatrix} 1\\ 2\\ 3\\ 4\\ \end{bmatrix}+x_2\begin{bmatrix} 1\\ 1\\ 1\\ 1\\ \end{bmatrix}+x_3\begin{bmatrix} 2\\ 3\\ 4\\ 5\\ \end{bmatrix}$

或者可以认为，Ax 代表着 A 的列空间。

显然，三个四维向量的线性组合是无法铺满整个四维空间的，就如同两个三维向量无法张开一个三维空间一样。所以，这里的 Ax 只能是 $R^4$ 空间的部分子空间，也就是说，无法保证任意拿出一个四维向量 $b=\begin{bmatrix} b_1\\ b_2\\ b_3\\ b_4\\ \end{bmatrix}\in R^4$ ，都能找到A列向量的一种线性组合，使 $Ax=b$ 。

第二个问题：什么样的 b 可以使方程 Ax=b 有解？

上面介绍过，Ax 就表示着 A 列向量的所有线性组合，也就是 A 的列空间。上面提到，A 的列空间就是 $R^4$ 的一个子空间，所以对于一个四维向量 b，只要 b 在“A 的列空间”这个 $R^4$ 的子空间中，那么就可以找到一种 A 列向量的线性组合来构成 b。也就是使得 Ax=b 有解。

第三个问题：能否去掉 A 的一列，却不影响 A 的列空间呢？

先看看这三个列向量： $\begin{bmatrix} 1\\ 2\\ 3\\ 4\\ \end{bmatrix}\begin{bmatrix} 1\\ 1\\ 1\\ 1\\ \end{bmatrix} \begin{bmatrix} 2\\ 3\\ 4\\ 5\\ \end{bmatrix}$ 。显然第三列 $\begin{bmatrix} 2\\ 3\\ 4\\ 5\\ \end{bmatrix}$ 可以写成前两列的线性组合： $\begin{bmatrix} 2\\ 3\\ 4\\ 5\\ \end{bmatrix}=\begin{bmatrix} 1\\ 2\\ 3\\ 4\\ \end{bmatrix}+\begin{bmatrix} 1\\ 1\\ 1\\ 1\\ \end{bmatrix}$ 。也就是说这第三列对线性组合没有贡献。所以我们仅依靠前两列的线性组合就可以构成A的列空间。我们称 $\begin{bmatrix} 1\\ 2\\ 3\\ 4\\ \end{bmatrix}\begin{bmatrix} 1\\ 1\\ 1\\ 1\\ \end{bmatrix}$ 这样的列为主列。所以去掉第三列，并不影响 A 的列空间的构成。

零空间

零空间介绍

所谓零空间，就是 $Ax=0$ 的所有解所构成的一个空间。

还是以 $A=\begin{bmatrix} 1 & 1 & 2\\ 2 & 1 & 3\\ 3 & 1 & 4\\ 4 & 1 & 5\\ \end{bmatrix}$ 为例，其零空间就是下面这个方程的解构成的空间：

$Ax=\begin{bmatrix} 1 & 1 & 2\\ 2 & 1 & 3\\ 3 & 1 & 4\\ 4 & 1 & 5\\ \end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ x_3\\ \end{bmatrix}=\begin{bmatrix} 0\\ 0\\ 0\\ 0\\ \end{bmatrix}=0$

也就是 $x=\begin{bmatrix} x_1\\ x_2\\ x_3\\ \end{bmatrix}$ ，可以看到x有三个分量，所以A的零空间是 $R^3$ 的子空间。

所以，对于 $m\times n$ 的矩阵来说，列空间是 $R^m$ 的子空间，零空间是 $R^n$ 的子空间。列空间关键在于列空间的维数，零空间关键在于列向量的个数。

首先来验证这样的 $\begin{bmatrix} x_1\\ x_2\\ x_3\\ \end{bmatrix}$ 为什么能构成向量空间？

加法封闭：在此零空间中任取两向量 v,w，有 Av=Aw=0，很显然 A(v+w)=0，所以(v+w)也属于零空间，加法封闭得证；
数乘封闭：在此零空间中任取向量 v，Av=0，则 cAv=0。矩阵 A 与常数 c 位置可交换，所以 A(cv)=0。所以 cv 也在零空间中。数乘运算封闭得证。

【例】求 $A=\begin{bmatrix} 1 & 1 & 2\\ 2 & 1 & 3\\ 3 & 1 & 4\\ 4 & 1 & 5\\ \end{bmatrix}$ 的零空间。

我们讨论过，这个 A 的第三列可以写成前两列的线性组合，所以可以写出令 Ax=0 的一个解： $\begin{bmatrix} 1\\ 1\\ -1\\ \end{bmatrix}$ ，而其零空间即为： $C\begin{bmatrix} 1\\ 1\\ -1\\ \end{bmatrix}$ (C表示任意常数)。反映在图像上，就是 $R^3$ 中的一条穿过原点的直线。

Ax=b 的空间解释

那如果上面构造零空间的方程右侧变为任意向量的话，其解集 x 还能构成向量空间吗？

如：

$\begin{bmatrix} 1 & 1 & 2\\ 2 & 1 & 3\\ 3 & 1 & 4\\ 4 & 1 & 5\\ \end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ x_3\\ \end{bmatrix}=\begin{bmatrix} 1\\ 2\\ 3\\ 4\\ \end{bmatrix}$

这样的所有 x 构成的解集还是向量空间吗？

显然不是。将 $\begin{bmatrix} x_1\\ x_2\\ x_3\\ \end{bmatrix}=\begin{bmatrix} 0\\ 0\\ 0\\ \end{bmatrix}$ 代入，其显然不是这个方程的解，就是说明这个解集里根本没有零向量。之前我们学过，任何一个向量集合中必须要有零向量。就是说明这个解集连最基本的要求都无法满足，构不成向量空间。

反映在图像上，这里所有的 $\begin{bmatrix} x_1\\ x_2\\ x_3\\ \end{bmatrix}$ 其实构成的是一个不过原点的平面。

这也告诉我们，想从 x 的角度研究 $Ax=b$ 这个方程，则只有 b 是零向量时，x 才能构成空间(零空间)，其他情况中连零向量都不在解集中，更别谈向量空间了。