Linear Algebra-投影矩阵与最小二乘-16

一、知识概要

本节聚焦于最小二乘法，深入探究上一节提及的投影概念。实际上，最小二乘法本质就是一种投影，其目的是使误差达到最小。同时，本节还涉及矩阵列空间与左零空间的相关知识，向量的投影就是在列空间中寻找距离最近的点，这与最小二乘法紧密相连。此外，还引出了标准正交向量组的概念。

二、投影矩阵回顾

上一节介绍了投影矩阵，其公式为：

在推导该公式时，，其中、是平面上的两个基，的列空间就是整个空间 。

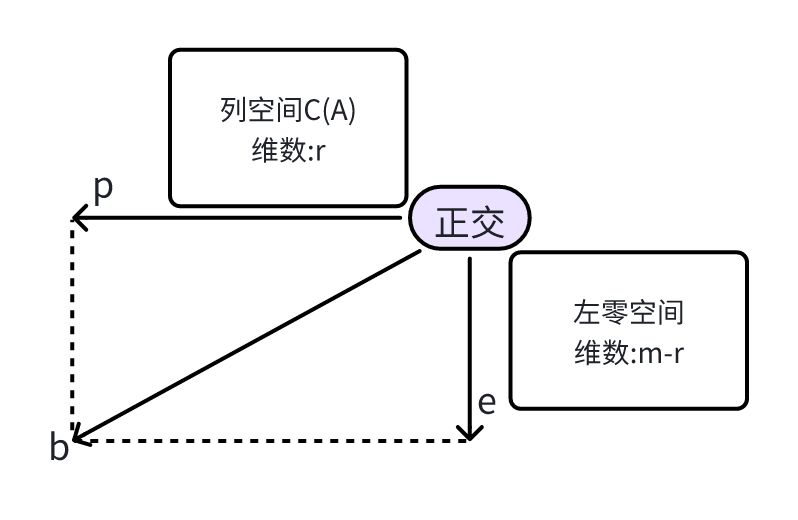
投影矩阵与向量的乘积，可以理解为将向量投影到它在列空间中的最近一点上。这和上节课将向量投影到平面上的过程类似。基于此，有以下两个问题：

  1. 若在矩阵的列空间里，则：此时。因为本身就在的列空间中，就如同上节课中向量就在平面上，投影就是其本身。

    • 证明过程：
      • 由于在的列空间里，所以一定可以写成的形式。
      • 将其代入投影矩阵可得：，根据矩阵乘法结合律，，而，所以，又因为，所以 。

  2. 若垂直于的列空间，则：此时，即没有投影。例如上节课中向量与平面垂直穿过的情况，此时向量在平面上没有分量，投影为 。

    • 证明过程：
      • 因为垂直于的列空间，所以垂直于的所有列向量，那么在左零空间中。
      • 代入投影矩阵，由于在左零空间，所以，则 。

通过这两个问题可知，一个向量总有两个分量，一个在的列空间中，另一个垂直于的列空间。投影矩阵的作用就是保留列空间中的分量，去除垂直于列空间的分量。可以用公式表示这种关系，其中是投影矩阵作用于上得到的向量，是左零空间中的分量。如果用类似投影矩阵表示，有，，这里可以把也看作一个投影矩阵，它将向量投影到左零空间中。

Linear_Algebra160

三、最小二乘法

3.1 最小二乘解题

【例】继续探讨上节课的例子，求解过三个点、、拟合的直线方程。

  1. 列出方程：假设最优直线方程为，将三个点代入可得方程组：

将其转化为矩阵方程的形式为：

很明显，这三个点不共线，该方程无解。

  1. 计算误差并拟合：由于三点不共线，先计算直线与各点之间的误差（偏移量），用表示。为便于计算，研究它们的平方和 。从几何意义上讲，这个过程本质是将向量投影到的列空间中，也就是将三个点投影到满足方程条件的最近的一条直线上。

使用上节课介绍的方程来拟合直线。在这个例子中，，，，代入方程求解：

则方程变为，求解可得：

所以得到的直线方程为 。

  1. 检验：分别将、、三个点的横坐标代入拟合直线方程，可以得到拟合直线上各点对应的位置，即的位置。需要注意的是，以上能使用最小二乘法是因为没有误差过大的量。

3.2 性质讨论

上述问题也可以通过使误差最小来计算。将误差化为，从导数的角度，对和求偏导并求极值，也能求得拟合直线。

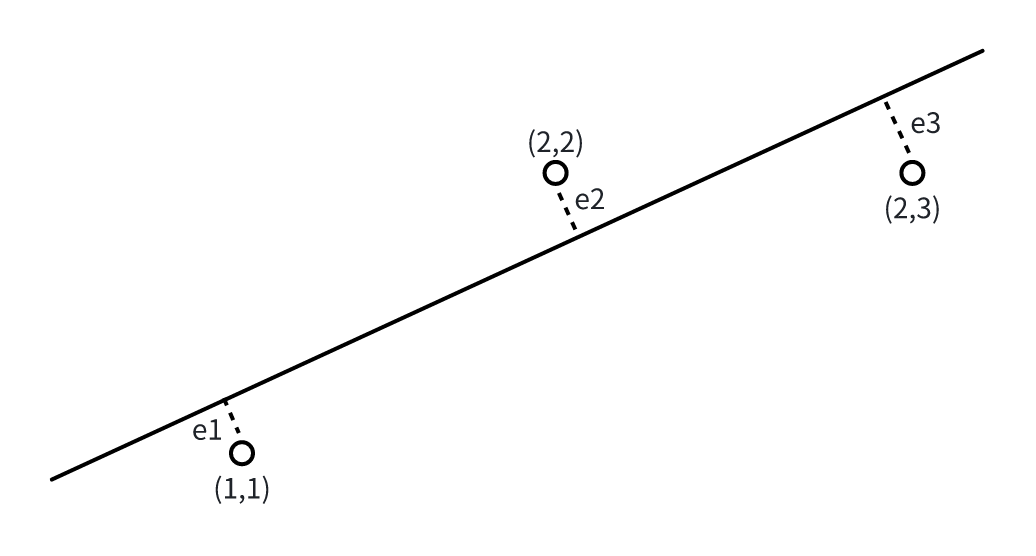
Linear_Algebra161

将误差向量记为，对应的投影向量记为（对应拟合直线上的值），有（为给定的点的实际值）。在本题中，，， 。由此可得到以下性质：

  1. 误差向量与投影向量垂直，即。
  2. 误差向量不仅垂直于，还垂直于列空间中的每一个向量。这些性质进一步验证了前文关于投影的相关介绍。

3.3 结论证明

在解方程过程中，用到了“如果矩阵各列线性无关，则矩阵可逆”这一结论，之前未给出证明，下面进行证明：

  1. 写出零空间方程形式，目的是寻找零空间内的向量 。

  2. 引入之前学过的结论：

    • 如果矩阵可逆，那么其对应的零空间仅包含零向量。
    • 对于列向量，表示求的长度。
    • 若，则（是列向量） 。

  3. 证明过程：

    • 将方程两边同时左乘，得到。
    • 根据矩阵乘法的性质，则。
    • 因为向量的内积，且向量的内积为 时，该向量为零向量，所以可推得。
    • 又因为已知矩阵各列线性无关，根据线性无关的定义，若，则必为零向量。
    • 综上，证得的零空间只有零向量，根据矩阵可逆的判定条件，若矩阵的零空间只有零向量，则该矩阵可逆，所以可逆。即证明了如果矩阵各列线性无关，则矩阵可逆。

四、标准正交基

这部分内容主要是为下节课做铺垫，相对较少，简单了解即可。

之前接触过的向量组，，，它们是正交的，并且还有特殊性质——都是单位向量，长度为 。基于此，引入“标准正交向量组”的概念，其中“标准”表示向量是单位向量。

同样属于标准正交向量组的还有，。

五、学习感悟

本节内容相互关联性强，最小二乘法与投影矩阵之间联系紧密，可以从多种角度进行理解。在学习过程中，记住将向量投影到列空间与左零空间的示意图非常重要，它有助于更牢固地掌握这部分知识。