Linear Algebra-子空间投影-15

一、知识概要

本节重点聚焦于投影相关知识，从向量投影出发，逐步拓展至高维投影，并以矩阵形式呈现投影。上一节介绍的正交概念在本节中有着重要应用，做投影本质上就是向另一个向量作垂线。通过本节学习，能深化对正交概念以及空间投影概念的理解。

二、投影

2.1 简单的投影

先来看简单投影的情况，如在下图中，向量是向量在向量上的投影，可表示为（为倍数） ，向量与投影的差值为。

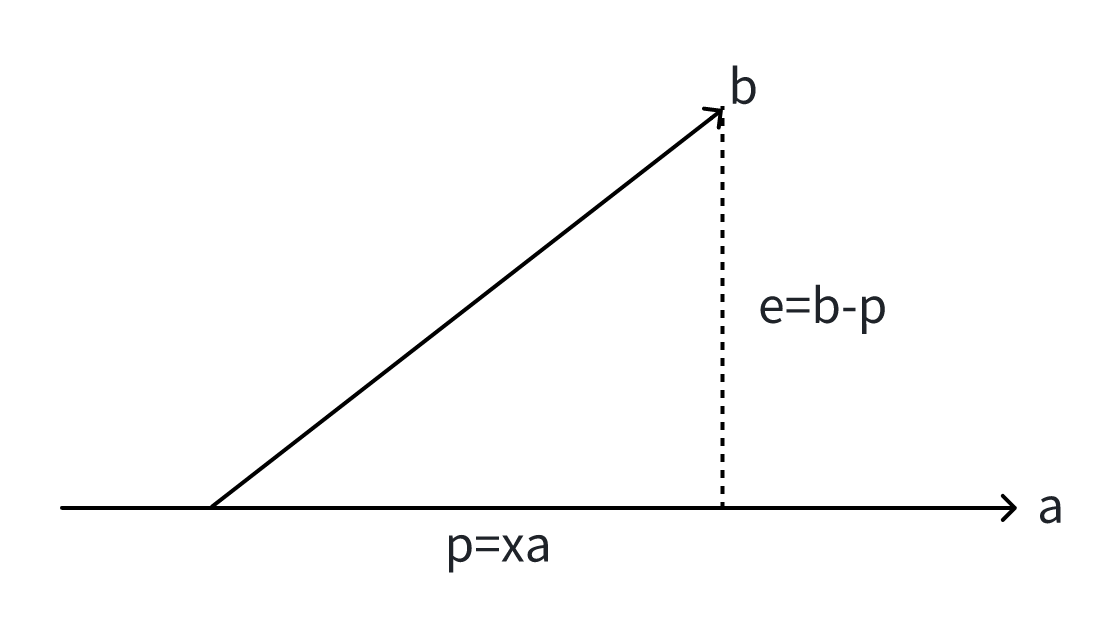
Linear_Algebra150

由向量与的垂直关系，结合上节正交概念，根据向量垂直时其点积为 ，可得：

求解上述关于的方程：

将代入，可得到：

从的表达式可以看出，投影是通过前面的系数（矩阵形式）来实现的，这个系数矩阵被称为投影矩阵，即（是投影矩阵，作用于向量上）。由此可得投影矩阵，该矩阵生成了投影。

需要注意的是，当是列向量时，是一个矩阵，是一个具体数字。在图一这种情况下，矩阵的秩为 且对称。这一结论可以通过具体计算或上一节末尾的相关结论得出。

投影矩阵具有两条重要性质：

  1. 对称性：。因为，分母是数字，分子转置后形式不变，所以是对称矩阵 。
  2. 幂等性：。从投影意义来看，如果对向量投影两次，其结果与只投影一次是一样的，所以投影矩阵满足。这两条性质是后续扩展投影概念的重要基础。

2.2 平面上的投影

在了解向量之间的投影后，进一步探讨向量与平面之间的投影。在下图中，，为构成平面的一组基，向量在该平面上，则可以表示为，也可写为，其中（都是列向量），。

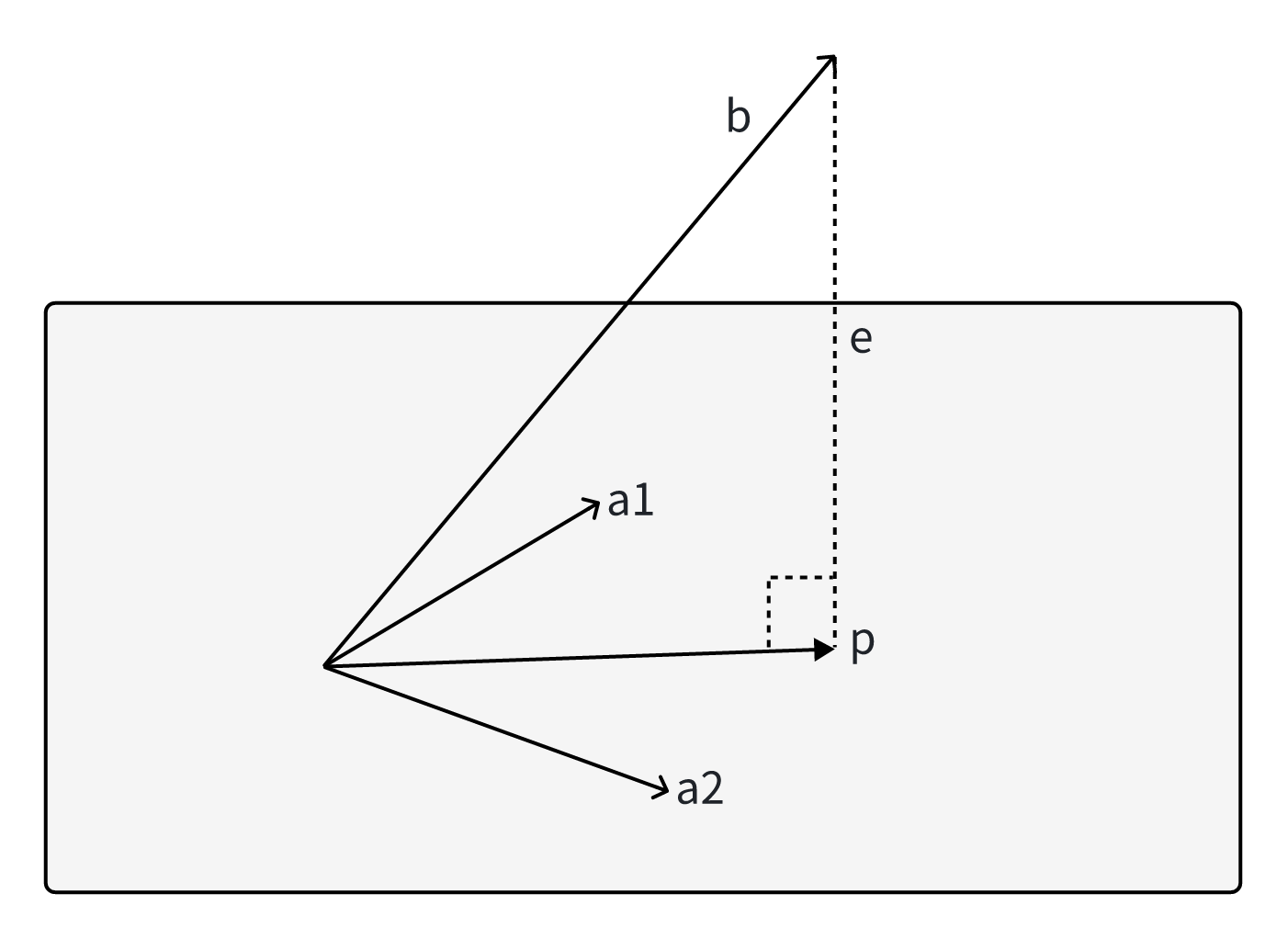
Linear_Algebra151

类比向量投影的思路，由于，都与向量垂直，将代入垂直关系可得：

将上述两个式子合写成矩阵形式为：

可以发现，该式与前面向量投影时得到的式子形式相似，实际上向量投影的式子是只有一列时的特殊情况。在这个式子中，（即垂直的向量）在的零空间里。根据上节课所学，零空间与行空间正交，所以向量与的行向量正交，进而与的列向量，正交，这在图中是显然成立的。

接下来求平面上的投影矩阵。由，先化简得到。这里需要注意，因为不一定是方阵，所以不能直接在两边左乘。但由于是由两个线性无关的基向量构成的矩阵，根据上节知识可知是可逆的，因此在两边同时左乘来解方程：

将代入，可得：

由此得到投影矩阵的表达式为：

这是投影矩阵的一般情况，而前面计算的是投影矩阵的一维特殊情况。同样，也具有和这两个性质，其证明过程与一维情况类似，在此不再详述，读者可以自行验证。

三、最小二乘法初涉

前面学习的投影知识有着重要的实际应用，其中投影中的可以看作向量与向量（或向量与平面）之间偏移量的大小，这为使用最小二乘法拟合直线提供了便利。

【例】求解过三个点，，拟合的直线方程。

  1. 列出方程：假设最优直线方程为，将三个点代入方程可得：
  1. 转化为矩阵方程并求解：将上述方程列成矩阵方程，发现该方程无解。此时运用投影中讲到的方法，将方程化为来求解。这种方法的关键在于，原本无解的方程，经过处理后得到的可以求出最优解，从而实现将无解的方程转换为可求解的最优方程。最小二乘法在后续课程中还会详细讲解。

四、学习感悟

本节内容是上一节正交知识的延伸。借助正交概念计算投影，并利用投影与向量之间的偏差引入最小二乘法，从而解决方程无解时的最优解问题，实现直线拟合。这部分内容实际应用性较强，核心目的是求解，以获得最优解。