线性代数12-矩阵应用:图与网络

Linear Algebra-矩阵应用:图与网络-12

一、知识概要

本节重点阐述图与矩阵之间的紧密联系，借助矩阵来展现图的特性。与前面几节内容不同，之前例子中的矩阵元素大多是为解释性质而设定的，而本节矩阵元素均源于实际问题，这能更直观地体现之前所学矩阵性质在实际场景中的应用价值。

二、图和关联矩阵

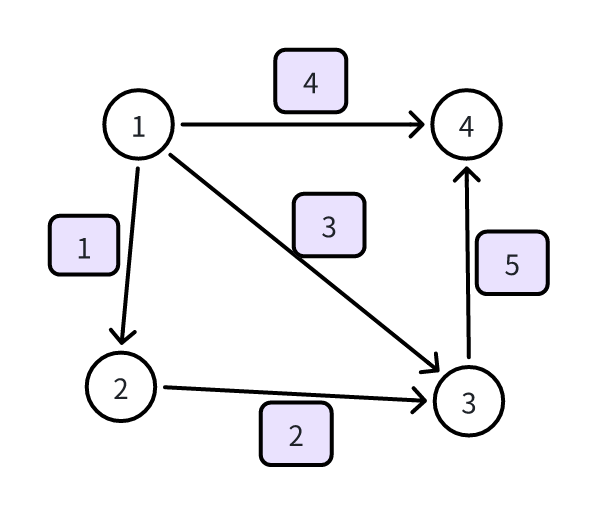
我们先来看一个有向图（图一）：

在本节中，我们围绕这个有向图展开研究。对于有向图，我们可以写出它的关联矩阵 $A$，如下：

$$A=\begin{bmatrix} -1 & 1 & 0 & 0 \\ 0 & -1 & 1 & 0 \\ -1 & 0 & 1 & 0 \\ -1 & 0 & 0 & 1 \\ 0 & 0 & -1 & 1 \end{bmatrix}$$

对于不太熟悉关联矩阵的读者，这里简单介绍一下。在这个 $5×4$ 的矩阵中，每一列对应一个节点，例如第一列代表节点 1，第二列代表节点 2，以此类推；每一行则代表一条边的走向，第一行代表边 1，第二行代表边 2，依此类推。需要注意的是，在每一行所代表的边中，若该边以某个节点为起点，那么在矩阵中对应元素为 -1；若以某个节点为终点，对应元素则为 1。

以第一行为例，第一行代表边 1 的特征。在图（一）中，边 1 从节点 1 出发，到达节点 2，这在矩阵中就表现为 $A_{11} = -1$，$A_{12} = 1$。其他行以此类推。

接下来，我们探讨图（一）所代表的实际意义。

【例】假设 $x$ 表示每个节点上的电势，研究 $Ax = b$ 这种形式能得出哪些结论。

1. 当 $b$为零向量时：此时需要求解 $Ax = 0$，即：

$$Ax=\begin{bmatrix} -1 & 1 & 0 & 0 \\ 0 & -1 & 1 & 0 \\ -1 & 0 & 1 & 0 \\ -1 & 0 & 0 & 1 \\ 0 & 0 & -1 & 1 \end{bmatrix}\begin{bmatrix}x_1 \\ x_2 \\ x_3 \\ x_4\end{bmatrix}=\begin{bmatrix}x_2 - x_1 \\ x_3 - x_2 \\ x_3 - x_1 \\ x_4 - x_1 \\ x_4 - x_3\end{bmatrix}=\begin{bmatrix}0 \\ 0 \\ 0 \\ 0 \\ 0\end{bmatrix}$$

求解上述方程组可得：$x = C\begin{bmatrix}1 \\ 1 \\ 1 \\ 1\end{bmatrix}$（$C$ 为常数）。

因为 $x$ 代表各个节点的电势，所以 $x$ 的解集表明当 $b = 0$ 时，各点电势必须相等。我们知道，电势差与电流的形成密切相关，$b = 0$ 意味着各条边上都没有电流（即电势差为零），而最终解得各点电势相等时边上电流为 0，这与我们的物理常识相符。

1. 当 $b$不为零时：我们可以通过特解加上通解的方法，求出在不同 $b$ 值情况下方程的解。这些解代表了在不同电势差情况下，各点电势的大小。

接下来研究左零空间 $A^T y = 0$ 的特点。首先，矩阵 $A$ 的转置为：

$$A^T=\begin{bmatrix} -1 & 0 & -1 & -1 & 0 \\ 1 & -1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & -1 \\ 0 & 0 & 0 & 1 & 1 \end{bmatrix}$$

然后求解方程 $A^T y = 0$，即：

$$A^T y=\begin{bmatrix} -1 & 0 & -1 & -1 & 0 \\ 1 & -1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & -1 \\ 0 & 0 & 0 & 1 & 1 \end{bmatrix}\begin{bmatrix}y_1 \\ y_2 \\ y_3 \\ y_4 \\ y_5\end{bmatrix}=\begin{bmatrix}0 \\ 0 \\ 0 \\ 0 \\ 0\end{bmatrix}$$

A转置后，$y$ 有五个分量，是对 $A^T$ 的行进行线性组合。由于 $A^T$ 的行代表 1 - 5 边，结合前面的例子背景，这里求解的就是流过每条边的电流。

求解该方程可得：

$$-y_1 - y_3 - y_4 = 0$$ $$y_1 - y_2 = 0$$ $$y_2 + y_3 - y_5 = 0$$ $$y_4 + y_5 = 0$$

这些方程体现了基尔霍夫定律，即每个节点流入和流出的电流相同。每个方程分别代表一个节点的电流情况，最终解得的 $\begin{bmatrix}y_1 & y_2 & y_3 & y_4 & y_5\end{bmatrix}$ 就是满足这一特性的各条边的电流值。

三、实际应用的扩展

$Ax = \begin{bmatrix}x_2 - x_1 & x_3 - x_2 & x_3 - x_1 & x_4 - x_1 & x_4 - x_3\end{bmatrix}$，这个式子表示每两点之间的电势差。该方程将图的特征（通过矩阵 $A$ 体现）与各点电势（x）紧密联系起来。

在研究 $A^T y$ 时，其中的 $y$ 代表各个边上的电流。结合电流与电势差的关系，我们联想到初中所学的欧姆定律。电流与电压之间存在一个比例系数，假设用矩阵 $C$ 表示，即有：

$\begin{bmatrix}y_1 \\ y_2 \\ y_3 \\ y_4\end{bmatrix}=C\begin{bmatrix}x_2 - x_1 \\ x_3 - x_2 \\ x_3 - x_1 \\ x_4 - x_3\end{bmatrix}=C Ax$，也就是 $y = CAx$。

这样，我们就成功地用矩阵表示了图像、电流和电势差这些概念。

进一步拓展，前面研究的 $A^T y = 0$ 是无源场的情况。如果存在外加电源，可表示为 $A^T y = f$（$f$ 表示外加电源的影响）。结合前面得到的 $y = CAx$，最终得到式子：$A^T CAx = f$。

四、学习感悟

本节内容与之前所学知识联系紧密，同时与实际应用的结合也十分紧密。从一个有向图出发，结合实际物理问题，详细解释了如何运用矩阵来阐述欧姆定律和基尔霍夫定律。学习完本节后，我们对之前所学的各种空间在实际问题中的作用有了更深入、更切实的理解，真正体会到线性代数知识的实用性和广泛应用。