卡诺图与最简SOP式

HDLBits链接

真值表

定义

真值表是表征逻辑事件输入和输出之间全部可能状态的表格。以1表示真，0表示假。

从真值表到标准式

  • SOP标准式：找出真值表中所有输出为1的表项，按照输入的情况，为1用变量表示，为0则用反变量表示，得出若干乘积项，然后求和。
  • POS标准式：找出真值表中所有输出为0的表项，按照输入的情况，为1用反变量表示，为0则用原变量表示，得出若干求和项，然后求积。

举例说明

有如下真值表

A B C D
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 1
1 0 1 0
1 1 0 1
1 1 1 1

若针对所有F=1的表项，可轻松写出SOP标准式如下：

F=ABC+ABC+ABC+ABC

若针对所有F=0的表项，可轻松写出POS标准式如下：

F=(A+B+C)(A+B+C)(A+B+C)(A+B+C)

从标准SOP式到最简SOP式

标准表达式并非最简表达式，从标准SOP式到最简SOP式为一个标准的逻辑化简的过程。

此时可以引入卡诺图，来寻找最小项的合并规律，从而可以轻易的进行化简工作，此处仅介绍系统化简法。

1、求出函数的SOP标准式

例如，对于函数：

F=ABC+ABC+D+ABCD

可写出其标准的SOP式为

1

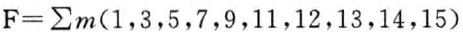
2、求出函数的全部主要项

首先，将最小项按其内部包含1的个数多少进行排列、分组，可得下表：

2

其次，根据该表，可以发现能合并的两个最小项必定位于相邻的两组，因此从最低组开始，和相邻高位组逐个运算合并，并按乘积项中1的个数进行排列得到的新表如下：(注：1、在合并的同时，需在之前的表中用勾标注出被使用过的最小项；2、如果合并结果与之前某次一样，则无需列出。)

3

第三，参考前两个步骤，继续对表项合并，直至无法合并为止。之后的合并过程需注意的是“—”的位置要相同，继续合并的结果如下：

4

5

第四，上述各表中，凡是没被“√”标记的合并项，就是主要项。对于该例，主要项就是：P0=AB和P1=D。

3、求出必要项、列出化简结果

如果某一个主要项中，至少包含一个其他项不包含的最小项，则它必然是必要项。

得到主要项后再进行验证是否存在等价主要项，并将其删除。

巩固练习

题目描述1：

实现下面卡诺图所描述的电路。

6

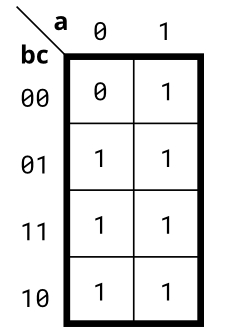
Solution1：

1
2
3
4
5
6
7
module top_module(
    input a,
    input b,
    input c,
    output out  ); 
    assign out = ~((~a)&(~b)&(~c));
endmodule

题目描述2：

实现下面卡诺图所描述的电路。

7

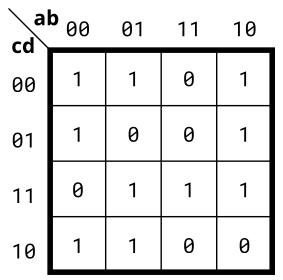
Solution2：

1
2
3
4
5
6
7
8
9
10
11
module top_module(
    input a,
    input b,
    input c,
    input d,
    output out  ); 

    assign out = ~a & ~d | ~b & ~c | b & c & d | a & c & d;
    
endmodule

题目描述3：

实现下面卡诺图所描述的电路。

8

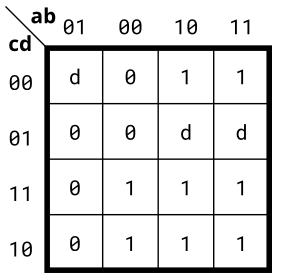
tips：d可以根据化简需求自己制定为0或是1。

Solution3：

1
2
3
4
5
6
7
8
9
10
module top_module(
    input a,
    input b,
    input c,
    input d,
    output out  ); 

    assign out =  a | (~a&~b&c);
    
endmodule

题目描述4：

实现下面卡诺图所描述的电路。

9

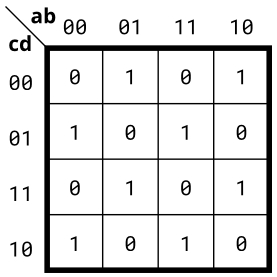
Solution4：

1
2
3
4
5
6
7
8
9
10
module top_module(
    input a,
    input b,
    input c,
    input d,
    output out  ); 

    assign out = a ^ b ^ c ^ d;
    
endmodule

题目描述5：

实现一个有四输入(a.b,c,d)的单输出数字系统，当2、7或15出现在输入端时，生成逻辑1，当0、1、4、5、6、9、10 13或14出现时，生成逻辑0。数字3、8、11和12的输入不会出现在这个系统中。例如，7对应于a和b。c,d分别被设为0,1,1,1。

确定最小SOP格式的输出out_sop和最小POS格式的输出out_pos。

Solution5：

1
2
3
4
5
6
7
8
9
10
11
12
13
module top_module (
    input a,
    input b,
    input c,
    input d,
    output out_sop,
    output out_pos
); 

    assign out_sop = c & d | ~a & ~b & c;
    assign out_pos = ~((~c | ~d) & (a | b | ~c));
    
endmodule

tips：这道题是最大项和最小项的问题，我们常用的是最小项，也就是积之和，但是最大项也需要了解一下，一般使用最小项就好了。

题目描述6：

实现下面卡诺图所描述的电路。

10

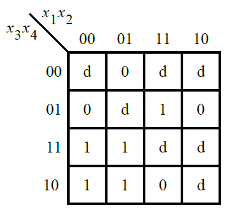
Solution6：

1
2
3
4
5
6
7
module top_module (
    input [4:1] x, 
    output f );

    assign f = ~x[1]&x[3] | x[2]&x[4];
    
endmodule

题目描述7：

实现下面卡诺图所描述的电路。

11

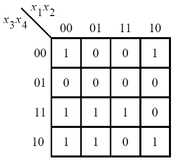
Solution7：

1
2
3
4
5
6
7
8
module top_module (
    input [4:1] x,
    output f
); 

    assign f = ~x[2]&~x[4] | ~x[1]&x[3] | x[2]&x[3]&x[4];
    
endmodule

题目描述8：

对于下面的卡诺图，用一个4-1多路选择器和不限的2-1多路选择器，但2-1多路选择器的使用要尽可能少。你不允许使用任何其他逻辑门，你必须使用a和b作为多路复用器选择器的输入，如下面的4- 1多路复用器所示。

12

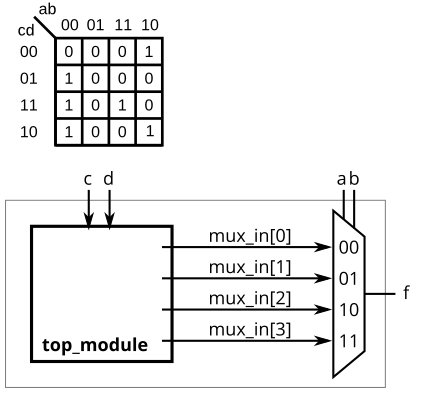
Solution8：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
module top_module (
    input c,
    input d,
    output [3:0] mux_in
);
    
    always @(*) begin
        case({c,d})
            2'b0:
                mux_in = 4'b0100;
            2'b1:
                mux_in = 4'b0001;
            2'b11:
                mux_in = 4'b1001;
            default:
                mux_in = 4'b0101;
        endcase
    end

endmodule

总结

  • 熟悉了卡诺图和基本的计算单元
  • 熟悉了卡诺图的化简方式，了解了SOP和POS的区别与联系，以及如何求得SOP最简式。